生成式扩散模型DDPM及其推导
把学习扩散模型DDPM的过程记录一下
为什么要写这篇?
工作中一直在做的是stable diffusion的优化,因此很想把diffusion到底是如何运行的机制彻底搞明白。在看的过程中发现,这块确实涉及到了很多数学知识,对我来说着实有些吃力,一些地方看的也不是很透彻。索性把学习过程中的知识做一下记录,加深一下印象。 这篇博客基本上就是把看到的文章摘抄一下。
什么是扩散模型?
扩散模型的灵感来自非平衡热力学。它们定义了一个马尔可夫链式扩散步骤,缓慢地向数据中添加随机噪声,然后学习逆扩散过程,从噪声中构建所需的数据样本。与变分自编码器 (VAE) 或流模型不同,扩散模型采用固定的学习过程,并且潜在变量具有高维性(与原始数据相同)。
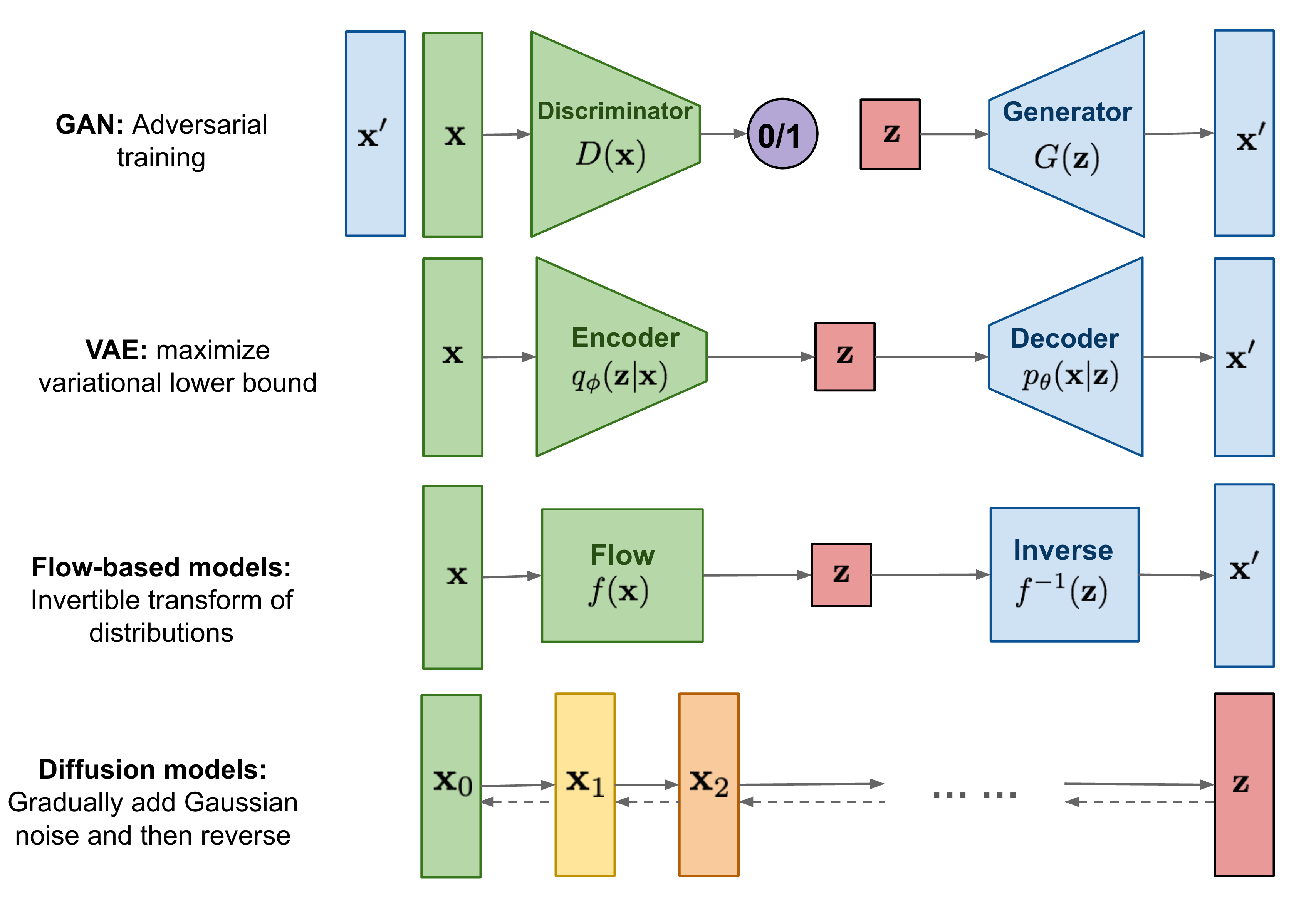
扩散模型的大火,是始于2020年所提出的DDPM(Denoising Diffusion Probabilistic Model),虽然也用了“扩散模型”这个名字,但事实上除了采样过程的形式有一定的相似之外,DDPM与传统基于朗之万方程采样的扩散模型可以说完全不一样,这完全是一个新的起点、新的篇章。
DDPM
苏神在文章
前向过程
给定一个样本数据\(x_0\)并假设其分布为\(q(x)\),即\(x_0 \sim q(x)\),定义一个前向扩散过程为分\(T\)步向样本添加少量高斯噪声,从而产生一系列噪声样本的过程,数据样本\(x_0\)随着步长\(t\)的增大,逐渐失去其可区分的特征。最终,当\(T \to \infty\)时,\(x_T\)等同于各向同性的高斯分布,这个就是“拆楼”的过程。
\begin{equation} x = x_0 \to x_1 \to x_2 \to \cdots x_{T-1} \to x_T = z \end{equation} 那么如何建模这个过程呢?
之前提到,前向扩散定义为不断的加入少量高斯噪声,得到一系列噪声的过程,那么假设:
\begin{equation} x_t=\alpha_t \boldsymbol{x}_{t-1}+\beta_t \varepsilon_t, \quad \varepsilon_t \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I}) \end{equation}
也就是可以理解为当前步等于上一步和一个高斯噪声的加权和,这里要求\(\alpha_t, \beta_t \ge 0\)且\({\alpha_t}^2 + {\beta_t}^2 = 1\)。 那么反复执行这个步骤,可以得到:
\[\begin{align} \boldsymbol{x}_t & =\alpha_t \boldsymbol{x}_{t-1}+\beta_t \varepsilon_t \nonumber \\ & =\alpha_t\left(\alpha_{t-1} \boldsymbol{x}_{t-2}+\beta_{t-1} \varepsilon_{t-1}\right)+\beta_t \varepsilon_t \nonumber \\ & =\cdots \nonumber \\ & =\left(\alpha_t \cdots \alpha_1\right) \boldsymbol{x}_0+\underbrace{\left(\alpha_t \cdots \alpha_2\right) \beta_1 \varepsilon_1+\left(\alpha_t \cdots \alpha_3\right) \beta_2 \varepsilon_2+\cdots+\alpha_t \beta_{t-1} \varepsilon_{t-1}+\beta_t \varepsilon_t}_{\text {多个相互独立的正态噪声之和 }} \end{align}\]正态分布具有叠加性,也就是说正态分布的和满足如下性质
那么上面的推导中的正态分布的和
\[\left(\alpha_t \cdots \alpha_2\right) \beta_1 \varepsilon_1+\left(\alpha_t \cdots \alpha_3\right) \beta_2 \varepsilon_2+\cdots+\alpha_t \beta_{t-1} \varepsilon_{t-1}+\beta_t \varepsilon_t\]变为均值为0(因为每个\(\varepsilon\)的均值为0)方差为 \(\left(\alpha_t \cdots \alpha_2\right)^2 \beta_1^2+\left(\alpha_t \cdots \alpha_3\right)^2 \beta_2^2+\cdots+\alpha_t^2 \beta_{t-1}^2+\beta_t^2\)的正态分布, 因为\({\alpha_t}^2 + {\beta_t}^2 = 1\),进而可以得到
\begin{equation} \left(\alpha_t \cdots \alpha_1\right)^2+\left(\alpha_t \cdots \alpha_2\right)^2 \beta_1^2+\left(\alpha_t \cdots \alpha_3\right)^2 \beta_2^2+\cdots+\alpha_t^2 \beta*{t-1}^2+\beta_t^2 = 1 \end{equation}
所以相当于有:
\[\begin{align} \boldsymbol{x}_t=\underbrace{\left(\alpha_t \cdots \alpha_1\right)}_{\text {记为 } \bar{\alpha}_t} \boldsymbol{x}_0+\underbrace{\sqrt{1-\left(\alpha_t \cdots \alpha_1\right)^2}}_{\text {记为 } \bar{\beta}_t} \bar{\varepsilon}_t, \quad \bar{\varepsilon}_t \sim \mathcal{N}(\mathbf{0}, \boldsymbol{I}) \end{align}\]采用另一种标记为
\begin{aligned} q(\mathbf{x_t}|\mathbf{x_0}) = \mathcal{N}(\mathbf{x_t}; \bar{\alpha_t} \mathbf{x}_0, \bar{\beta_t}^2 \boldsymbol{I}) \end{aligned}
意思是在\(x_0\)已知的情况下,\(x_t\)服从上述概率分布。
上述式子是苏神文章中
令\(\bar{\alpha}_t=\prod_{i=1}^t \alpha_i, \alpha_t = 1 - \beta_t\), 那么苏神的推导中的式子最终变为:
\begin{equation} q(\mathbf{x_t}|\mathbf{x_0}) = \mathcal{N}(\mathbf{x_t}; \sqrt{ \bar{\alpha_t} } \mathbf{x}_0, (1-\bar{\alpha_t}) \boldsymbol{I}) \end{equation}
逆向过程
DDPM要做的事情,就是从上述信息中求出反向过程所需要的\(q(x_{t−1} \mid x_t)\),这样我们就能实现从任意一个\(x_T=z\)出发,逐步采样出\(x_{T−1},x_{T−2}, \cdots , x_1\),最后得到随机生成的样本数据\(x_0=x\)。
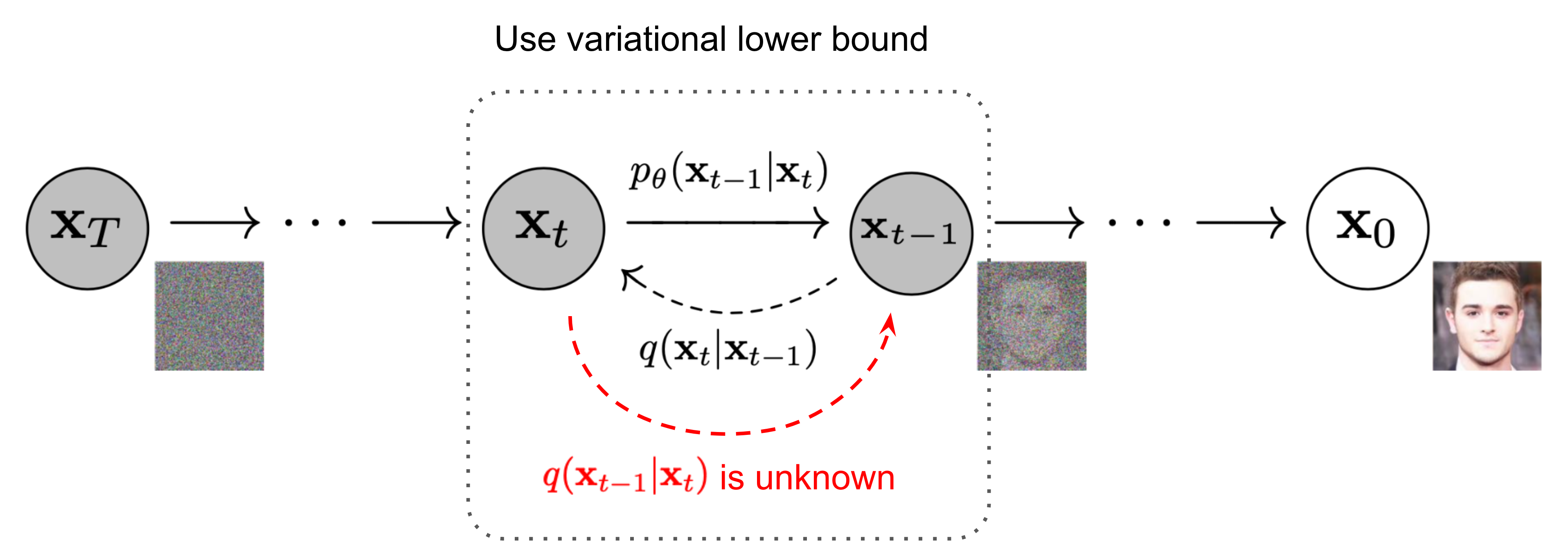
为了求\(q(x_{t−1} \mid x_t)\),直接根据贝叶斯定理我们有
然而,我们并不知道\(q(x_{t−1}), q(x_t)\)的表达式,所以此路不通。但我们可以退而求其次,在给定\(x_0\)的条件下使用贝叶斯定理 由于扩散核本身不依赖 \(x_0\) 所以\(q\left(\boldsymbol{x}_{t} \mid \boldsymbol{x}_{t-1},x_0\right) = q\left(\boldsymbol{x}_{t} \mid \boldsymbol{x}_{t-1}\right)\) :
\[q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t, \boldsymbol{x}_0\right)=\frac{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}, \boldsymbol{x}_0\right) q\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_0\right)}{q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_0\right)}\]其中根据式(6)得到
\[\begin{aligned} q(\mathbf{x_t}|\mathbf{x_0}) & = \mathcal{N}(\mathbf{x_t}; \sqrt{ \bar{\alpha_t} } \mathbf{x}_0, (1-\bar{\alpha_t}) \boldsymbol{I}) \\ q(\mathbf{x_{t-1}}|\mathbf{x_0}) & = \mathcal{N}(\mathbf{x_{t-1}}; \sqrt{ \bar{\alpha}_{t-1} } \mathbf{x}_0, (1-\bar{\alpha}_{t-1}) \boldsymbol{I}) \\ q(\mathbf{x_{t}}|\mathbf{x_{t-1}},\mathbf{x_0}) & = \mathcal{N}(\mathbf{x_t}; \sqrt{ \alpha_t } \mathbf{x}_{t-1}, \beta_t \boldsymbol{I}) \\ \end{aligned}\]这里需要注意的是
\[q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \tilde{\boldsymbol{\mu}}(\mathbf{x}_t, \mathbf{x}_0), \tilde{\beta_t} \mathbf{I})\]公式表示的是在已知\(\mathbf{x}_0\) 和\(\mathbf{x}_t\)的情况下,描述\(\mathbf{x}_{t-1}\)的分布,因此公式中的期望是和\(\mathbf{x}_0\) 及 \(\mathbf{x}_t\)相关的。
那么可以继续推导如下:
\[\begin{align*} q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) &= q(\mathbf{x}_t \mid \mathbf{x}_{t-1}, \mathbf{x}_0) \cdot \frac{q(\mathbf{x}_{t-1} \mid \mathbf{x}_0)}{q(\mathbf{x}_t \mid \mathbf{x}_0)} \\ &\propto \exp\left(-\frac{1}{2} \left( \frac{(\mathbf{x}_t - \sqrt{\alpha_t} \mathbf{x}_{t-1})^2}{\beta_t} + \frac{(\mathbf{x}_{t-1} - \sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0)^2}{1 - \bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1 - \bar{\alpha}_t} \right)\right) \\ &= \exp\left(-\frac{1}{2} \left( \frac{\mathbf{x}_t^2 - 2\sqrt{\alpha_t} \mathbf{x}_t \mathbf{x}_{t-1} + \alpha_t \mathbf{x}_{t-1}^2}{\beta_t} + \frac{\mathbf{x}_{t-1}^2 - 2\sqrt{\bar{\alpha}_{t-1}} \mathbf{x}_0 \mathbf{x}_{t-1} + \bar{\alpha}_{t-1} \mathbf{x}_0^2}{1 - \bar{\alpha}_{t-1}} - \frac{(\mathbf{x}_t - \sqrt{\bar{\alpha}_t} \mathbf{x}_0)^2}{1 - \bar{\alpha}_t} \right)\right) \\ &= \exp\left( -\frac{1}{2} \left( \left( \frac{\alpha_t}{\beta_t} + \frac{1}{1 - \bar{\alpha}_{t-1}} \right) \mathbf{x}_{t-1}^2 - \left( \frac{2\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t + \frac{2\sqrt{\bar{\alpha}_{t-1}}}{1 - \bar{\alpha}_{t-1}} \mathbf{x}_0 \right) \mathbf{x}_{t-1} + C(\mathbf{x}_t, \mathbf{x}_0) \right) \right) \end{align*}\]这里的\(C(\mathbf{x}_t, \mathbf{x}_0)\)和\(\mathbf{x}_{t-1}\)是无关的因此看成常数项,这里 \(\alpha_t=1-\beta_t\)
继续推导得到:
\[\begin{aligned} \tilde{\beta}_t & =1 /\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right)=1 /\left(\frac{\alpha_t-\bar{\alpha}_t+\beta_t}{\beta_t\left(1-\bar{\alpha}_{t-1}\right)}\right)=\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t \\ \tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right) & =\left(\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) /\left(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar{\alpha}_{t-1}}\right) \\ & =\left(\frac{\sqrt{\alpha_t}}{\beta_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}}}{1-\bar{\alpha}_{t-1}} \mathbf{x}_0\right) \frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t \\ & =\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0 \end{aligned}\]也就是:
\[\begin{align} q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0) = \mathcal{N}(\mathbf{x}_{t-1}; \frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \mathbf{x}_0,\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t) \end{align}\]根据式(5)得到 \(\mathbf{x}_0=\frac{1}{\sqrt{\bar{\alpha}_t}}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t\right)\) ,继而得到:
\[\begin{aligned} \tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right) \approx \tilde{\boldsymbol{\mu}}_t & =\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}}_t}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t\right) \\ \end{aligned}\]需要注意的是这个地方\(\bar{\alpha}_t=\prod_{i=1}^t \alpha_i\),所以公式可以这么推导:
\[\begin{aligned} \tilde{\boldsymbol{\mu}}_t & =\frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}}_t}\left(\mathbf{x}_t-\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t\right) \\ & = \frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}}_t} \mathbf{x}_t- \frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}}_t} \sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t \\ & = \frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}}_t} \mathbf{x}_t- \frac{ \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\alpha}_t} \sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t \\ & = \frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}}_t} \mathbf{x}_t- \frac{ 1 - {\alpha}_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\alpha}_t} \sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t \\ & = \frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\sqrt{\bar{\alpha}_{t-1}} \beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\bar{\alpha}}_t} \mathbf{x}_t- \frac{ 1 - {\alpha}_t}{\sqrt{1-\bar{\alpha}_t}} \frac{1}{\sqrt{\alpha}_t} \boldsymbol{\epsilon}_t \\ & = \frac{\sqrt{\alpha_t}\left(1-\bar{\alpha}_{t-1}\right)}{1-\bar{\alpha}_t} \mathbf{x}_t+\frac{\beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\alpha}_t} \mathbf{x}_t- \frac{ 1 - {\alpha}_t}{\sqrt{1-\bar{\alpha}_t}} \frac{1}{\sqrt{\alpha}_t} \boldsymbol{\epsilon}_t \\ & = \frac{\alpha_t \left(1-\bar{\alpha}_{t-1}\right)}{\sqrt{\alpha_t}(1-\bar{\alpha}_t)} \mathbf{x}_t+\frac{\beta_t}{1-\bar{\alpha}_t} \frac{1}{\sqrt{\alpha}_t} \mathbf{x}_t- \frac{ 1 - {\alpha}_t}{\sqrt{1-\bar{\alpha}_t}} \frac{1}{\sqrt{\alpha}_t} \boldsymbol{\epsilon}_t \\ & = \frac{\alpha_t \left(1-\bar{\alpha}_{t-1}\right) + \beta_t}{\sqrt{\alpha_t}(1-\bar{\alpha}_t)} \mathbf{x}_t- \frac{ 1 - {\alpha}_t}{\sqrt{1-\bar{\alpha}_t}} \frac{1}{\sqrt{\alpha}_t} \boldsymbol{\epsilon}_t \\ & = \frac{\alpha_t + \beta_t -\alpha_t \bar{\alpha}_{t-1} }{\sqrt{\alpha_t}(1-\bar{\alpha}_t)} \mathbf{x}_t- \frac{ 1 - {\alpha}_t}{\sqrt{1-\bar{\alpha}_t}} \frac{1}{\sqrt{\alpha}_t} \boldsymbol{\epsilon}_t \\ & = \frac{1 -\bar{\alpha}_{t} }{\sqrt{\alpha_t}(1-\bar{\alpha}_t)} \mathbf{x}_t- \frac{ 1 - {\alpha}_t}{\sqrt{1-\bar{\alpha}_t}} \frac{1}{\sqrt{\alpha}_t} \boldsymbol{\epsilon}_t \\ & = \frac{1}{\sqrt{\alpha_t}} \mathbf{x}_t- \frac{ 1 - {\alpha}_t}{\sqrt{1-\bar{\alpha}_t}} \frac{1}{\sqrt{\alpha}_t} \boldsymbol{\epsilon}_t \\ & =\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_t\right) \end{aligned}\]也就是 \(\begin{align} q(\mathbf{x}_{t-1} \mid \mathbf{x}_t) = \mathcal{N}(\mathbf{x}_{t-1}; \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_t\right) ,\frac{1-\bar{\alpha}_{t-1}}{1-\bar{\alpha}_t} \cdot \beta_t) \end{align}\)
训练
现在我们已经知道了\(q(\mathbf{x}_{t-1} \mid \mathbf{x}_t)\),也就是在\(x_t\)已知情况下的\(x_{t-1}\)的分布,那么我们想要学习的是学一个「逆过程」的近似分布,也就是说学习如下过程:
\[p_{\theta}(\mathbf{x}_{t-1} \mid \mathbf{x}_t) \approx q(\mathbf{x}_{t-1} \mid \mathbf{x}_t, \mathbf{x}_0)\]既然是学习,那么也就有个损失函数,关于这个损失函数的由来,也是有理论的分析,给定一个训练集的数据\(x_0\),经过前向过程和反向过程,扩散模型要让复原出\(x_0\)的概率尽可能大,也就是最大化\(p_{\theta}(\mathbf{x}_{0})\)的过程,这个优化目标会转变成优化一个叫做变分下(variational lower bound, VLB)的量,具体的推导我这里就不列了,可以参考博客
最终我们会得到损失函数:
\[\begin{aligned} L_t & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{1}{2\left\|\boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right\|_2^2}\left\|\tilde{\boldsymbol{\mu}}_t\left(\mathbf{x}_t, \mathbf{x}_0\right)-\boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{1}{2\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_t\right)-\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{\left(1-\alpha_t\right)^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right\|^2\right] \\ & =\mathbb{E}_{\mathbf{x}_0, \boldsymbol{\epsilon}}\left[\frac{\left(1-\alpha_t\right)^2}{2 \alpha_t\left(1-\bar{\alpha}_t\right)\left\|\boldsymbol{\Sigma}_\theta\right\|_2^2}\left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right\|^2\right]\end{aligned}\]DDPM论文指出,如果把前面的系数全部丢掉的话,模型的效果更好。最终,我们就能得到一个非常简单的优化目标:
\[\begin{align} \left\|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}_t, t\right)\right\|^2 \end{align}\]那么知道了这些该如何训练这个扩散模型呢?
你有 5000 张干净的图像,训练目标是让模型通过这些图像学会“如何一步步把噪声还原成原图”。训练的大概流程如下:
- 随机选择一张图像,假设为\(x_0\)
- 随机选一个时间步t, \(t \in {1,2,..., T}\)
- 随机采样一个高斯噪声量,与\(x_0\)形状一致。
-
使用如下公式进行加噪:
\[x_t = \sqrt{\bar{\alpha_{t}}} x_0 + \sqrt{1 - \bar{\alpha_{t}}} \boldsymbol{\epsilon}\]其中\(\bar{\alpha_{t}}\)由你预设的“噪声调度表”提供,是每一步的衰减因子
- 把\(x_t\) 和t输入到模型(比如UNet),输出\(\boldsymbol{\epsilon}_{\theta}(x_t,t)\)
- 利用损失函数(7),计算损失并优化网络,更新权重
推理
训练完成模型之后,我们得到了模型,也就是说得到了拟合的反向过程的分布,那么推理的时候就是从一个随机噪声中一步步还原生成图像的过程。实际上我们训练的模型估计是\(\boldsymbol{\epsilon}_{\theta}(x_t,t)\), 那么根据公式:
\[\begin{aligned} \boldsymbol{\mu}_\theta\left(\mathbf{x}_t, t\right) & =\frac{1}{\sqrt{\alpha_t}}\left(\mathrm{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon_\theta\left(\mathrm{x}_t, t\right)\right) \\ \text { Thus } \mathbf{x}_{t-1} & =\mathcal{N}\left(\mathbf{x}_{t-1} ; \frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right), \boldsymbol{\Sigma}_\theta\left(\mathbf{x}_t, t\right)\right)\end{aligned}\]可以得到推理中的采样过程为:
\[\begin{aligned} &\text { Algorithm } 2 \text { Sampling }\\ \hline &\mathbf{x}_T \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\\ &\text { for } t=T, \ldots, 1 \text { do }\\ &\mathbf{z} \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) \text { if } t>1 \text {, else } \mathbf{z}=\mathbf{0}\\ &\mathbf{x}_{t-1}=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{1-\alpha_t}{\sqrt{1-\bar{\alpha}_t}} \boldsymbol{\epsilon}_\theta\left(\mathbf{x}_t, t\right)\right)+\sigma_t \mathbf{z}\\ &\text { end for }\\ &\text { return } \mathrm{x}_0 \\ \hline \end{aligned}\]其中每次加上随机噪声\(\sigma_t\)是为了加回一点随机性,以保证整个生成过程的多样性和概率分布的正确性。