接着上篇对Attention的基础分析之后，继续来整理一下FlashAttention系列。

FlashAttention1

为什么？

要介绍为什么，也就是解释FlashAttention1解决了什么问题？

我们知道Attention的计算如下：

\[\mathbf{S}=\mathbf{Q} \mathbf{K}^{\top} \in \mathbb{R}^{N \times N}, \quad \mathbf{P}=\operatorname{softmax}(\mathbf{S}) \in \mathbb{R}^{N \times N}, \quad \mathbf{O}=\mathbf{P V} \in \mathbb{R}^{N \times d},\]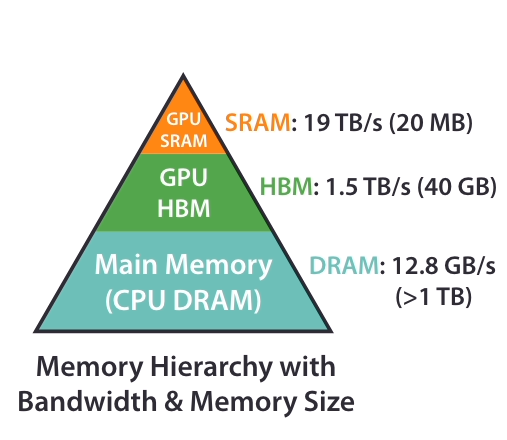

⊕
GPU中显存结构和带宽示意图

对于中间计算矩阵\(\mathbf{S}\)，它的维度是\({N \times N}\)，这个矩阵维度很大，存储在HBM中需要\(\mathbf{O}(N^2)\)的显存，例如对GPT2来说\(N = 1024，d = 64\)，假设是float16计算，需要的显存是\(1024 \times 1024 \times sizeof(float16) = 2 \mathbf{M}\)，如果\(N = 102400\) 也就是100K的长度，占用的显存就是\(102400 \times 102400 \times sizeof(float16) = 20 \mathbf{G}\)。这在长序列中显然带来显存上的瓶颈。

原始的标准Attention的计算方式如下：

\[\begin{array}{l} \hline &\text { Algorithm } 0 \text { Standard Attention Implementation }\\ \hline &\text { Require: Matrices } \mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d} \text { in } \mathrm{HBM} \text {. }\\ \hline &\text { Load } \mathbf{Q}, \mathbf{K} \text { by blocks from HBM, compute } \mathbf{S}=\mathbf{Q} \mathbf{K}^{\top} \text {, write } \mathbf{S} \text { to HBM. }\\ \hline &\text { Read } \mathbf{S} \text { from HBM, compute } \mathbf{P}=\operatorname{softmax}(\mathbf{S}) \text {, write } \mathbf{P} \text { to HBM. }\\ \hline &\text { Load } \mathbf{P} \text { and } \mathbf{V} \text { by blocks from HBM, compute } \mathbf{O}=\mathbf{P V} \text {, write } \mathbf{O} \text { to HBM. }\\ \hline &\text { Return } 0 . \\ \hline \end{array}\]

从算法中可以看出，原始的Attention算法需要将完整的Q和K矩阵从HBM中分块读取到SM上进行矩阵乘法。计算得到的中间结果S被完整写回到HBM，再次从HBM读取S矩阵，对每一行应用softmax操作得到P矩阵，然后再次将P写回HBM。从HBM中读取P和V，进行矩阵乘法，得到最终的输出O。O也是写回HBM。由于每一步都需要从HBM读入矩阵数据、计算后再写回，造成了大量的内存带宽消耗。这在实际硬件上往往成为Attention推理或训练的性能瓶颈。

正是为了缓解上述两个问题，FlashAttention1提出了一种改进的Attention计算方式，通过块状处理（tiling），避免显存中存储完整的S或P矩阵，大幅降低了内存占用和带宽压力，从而实现了更高效的Attention计算。

是什么？

\[\begin{array}{ll} \hline & &\text { Algorithm } 1 \text { FlashAttention }\\ \hline & &\text { Require: Matrices } \mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d} \text { in HBM, on-chip SRAM of size } M \text {. }\\ &1: &\text { Set block sizes } B_c=\left\lceil\frac{M}{4 d}\right\rceil, B_r=\min \left(\left\lceil\frac{M}{4 d}\right\rceil, d\right) \text {. }\\ &2: &\text { Initialize } \mathbf{O}=(0)_{N \times d} \in \mathbb{R}^{N \times d}, \ell=(0)_N \in \mathbb{R}^N, m=(-\infty)_N \in \mathbb{R}^N \text { in HBM. }\\ &3: &\text { Divide } \mathbf{Q} \text { into } T_r=\left\lceil\frac{N}{B_r}\right\rceil \text { blocks } \mathbf{Q}_1, \ldots, \mathbf{Q}_{T_r} \text { of size } B_r \times d \text { each, and divide } \mathbf{K}, \mathbf{V} \text { in to } T_c=\left\lceil\frac{N}{B_c}\right\rceil \text { blocks }\\ & & \mathbf{K}_1, \ldots, \mathbf{K}_{T_c} \text { and } \mathbf{V}_1, \ldots, \mathbf{V}_{T_c} \text {, of size } B_c \times d \text { each. }\\ &4: &\text { Divide } \mathbf{O} \text { into } T_r \text { blocks } \mathbf{O}_i, \ldots, \mathbf{O}_{T_r} \text { of size } B_r \times d \text { each, divide } \ell \text { into } T_r \text { blocks } \ell_i, \ldots, \ell_{T_r} \text { of size } B_r \text { each, }\\ & & \text { divide } m \text { into } T_r \text { blocks } m_1, \ldots, m_{T_r} \text { of size } B_r \text { each. }\\ &5: &\text { for } 1 \leq j \leq T_c \text { do }\\ &6: &\quad \text { Load } \mathbf{K}_j, \mathbf{V}_j \text { from HBM to on-chip SRAM. }\\ &7: &\quad \text { for } 1 \leq i \leq T_r \text { do }\\ &8: &\qquad\text { Load } \mathbf{Q}_i, \mathbf{O}_i, \ell_i, m_i \text { from HBM to on-chip SRAM. }\\ &9: &\qquad\text { On chip, compute } \mathbf{S}_{i j}=\mathbf{Q}_i \mathbf{K}_j^T \in \mathbb{R}^{B_r \times B_c} \text {. }\\ &10: &\qquad\text { On chip, compute } \tilde{m}_{i j}=\operatorname{rowmax}\left(\mathbf{S}_{i j}\right) \in \mathbb{R}^{\boldsymbol{B}_r}, \tilde{\mathbf{P}}_{i j}=\exp \left(\mathbf{S}_{i j}-\tilde{m}_{i j}\right) \in \mathbb{R}^{\boldsymbol{B}_r \times \boldsymbol{B}_{\boldsymbol{C}}} \text { (pointwise), } \tilde{\ell}_{i j}= \text { rowsum }\left(\tilde{\mathbf{P}}_{i j}\right) \in \mathbb{R}^{B_r} \text {. }\\ &11: &\qquad\text { On chip, compute } m_i^{\text {new }}=\max \left(m_i, \tilde{m}_{i j}\right) \in \mathbb{R}^{B_r}, \ell_i^{\text {new }}=e^{m_i-m_i^{\text {new }}} \ell_i+e^{\tilde{m}_{i j}-m_i^{\text {new }}} \tilde{\ell}_{i j} \in \mathbb{R}^{B_r} \text {. }\\ &12: &\qquad\text { Write } \mathbf{O}_i \leftarrow \operatorname{diag}\left(\ell_i^{\text {new }}\right)^{-1}\left(\operatorname{diag}\left(\ell_i\right) e^{m_i-m_i^{\text {new }}} \mathbf{O}_i+e^{\tilde{m}_{i j}-m_i^{\text {new }}} \tilde{\mathbf{P}}_{i j} \mathbf{V}_j\right) \text { to HBM. }\\ &13: &\qquad\text { Write } \ell_i \leftarrow \ell_i^{\text {new }}, m_i \leftarrow m_i^{\text {new }} \text { to HBM. }\\ &14: &\quad\text { end for }\\ &15: &\text { end for }\\ &16: &\text { Return } \mathbf{0} \text {. }\\ \hline \end{array}\]

我在一开始看这个算法的时候，感觉不是很直观，大概知道它在做一些事情，但是不能够完全明白。实际上在原论文中把这部分的贡献叫做Kernel Fusion，也就是算子融合，核心是通过矩阵分块和算子融合，来减少显存和带宽的压力。其中有两个部分的关键点，一个是online softmax，一个是矩阵的tiling，下面我们会一一详细解释。

怎么做？

online softmax

如果采用矩阵分块，首先会想到，Attention的softmax是如何操作，因为矩阵分块之后，得到的\(\mathbf{S}=\mathbf{Q} \mathbf{K}^{\top}\) 应该也是分块的，而softmax是按行进行操作的，如何正确的处理softmax操作，这个就是online softmaxsee From Online Softmax to FlashAttention 算法解决的问题。

先看softmax的操作：

对于向量 \(\mathbf{x} = (x_0,x_1,\ldots, x_n)\), 令\(\mathbf{m} = max(x_0,x_1,\ldots, x_n)\), 那么:

\[softmax(\mathbf{x}) = \frac{(e^{x_0-m},e^{x_1-m},\ldots, e^{x_n-m})}{ \sum{(e^{x_0-m},e^{x_1-m},\ldots, e^{x_n-m})} }\]

采用论文中的标记就是:

\[m(x):=\max _i \quad x_i, \quad f(x):=\left[\begin{array}{lll} e^{x_1-m(x)} & \ldots & e^{x_B-m(x)} \end{array}\right], \quad \ell(x):=\sum_i f(x)_i, \quad \operatorname{softmax}(x):=\frac{f(x)}{\ell(x)} .\]

对于softmax过程中，影响分块的其实是分母上的和，它需要计算整个向量，假设对于\(\ell = \sum_{j=1}^{N} { e^{x_j - m} }\), 那么有如下递推关系：

\[\begin{array}{l} \ell_i = \sum_{j=1}^{i} { e^{x_j - m_i} } \\ \ell_{i+1} = \sum_{j=1}^{i+1} { e^{x_j - m_{i+1}} } \\ \ell_{i+1} = \sum_{j=1}^{i} { e^{x_j - m_{i+1}} } + e^{x_{i+1} - m_{i+1}} \\ \ell_{i+1} = \sum_{j=1}^{i} { e^{x_j - m_{i} + m_{i} - m_{i+1}} } + e^{x_{i+1} - m_{i+1}} \\ \ell_{i+1} = e^{m_{i} - m_{i+1}} \sum_{j=1}^{i} { e^{x_j - m_{i} } } + e^{x_{i+1} - m_{i+1}} \\ \ell_{i+1} = e^{m_{i} - m_{i+1}} \ell_{i} + e^{x_{i+1} - m_{i+1}} \\ \end{array}\]

根据这个递推关系可以知道，最终的分母上的和可以由开始的时候递推获取，不需要等到所有的数据准备好在计算。根据这个递推关系，很容易知道，对于分块的向量：

\[\begin{array}{l} & m(x) = m\left(\left[x^{(1)} \ x^{(2)}\right]\right) = \max(m(x^{(1)}), m(x^{(2)})) \\ & f(x) = \left[e^{m(x^{(1)}) - m(x)} f(x^{(1)}) \quad e^{m(x^{(2)}) - m(x)} f(x^{(2)})\right] \\ & \ell(x) = \ell\left([x^{(1)} \ x^{(2)}]\right) = e^{m(x^{(1)}) - m(x)} \ell(x^{(1)}) + e^{m(x^{(2)}) - m(x)} \ell(x^{(2)}) \\ & \text{softmax}(x) = \frac{f(x)}{\ell(x)}. \end{array}\]

因此对于分块的矩阵或分块向量，只需要记录和更新对应的\((m{(x)},\ell{(x)})\),就能正确的计算最终的结果。

tiling

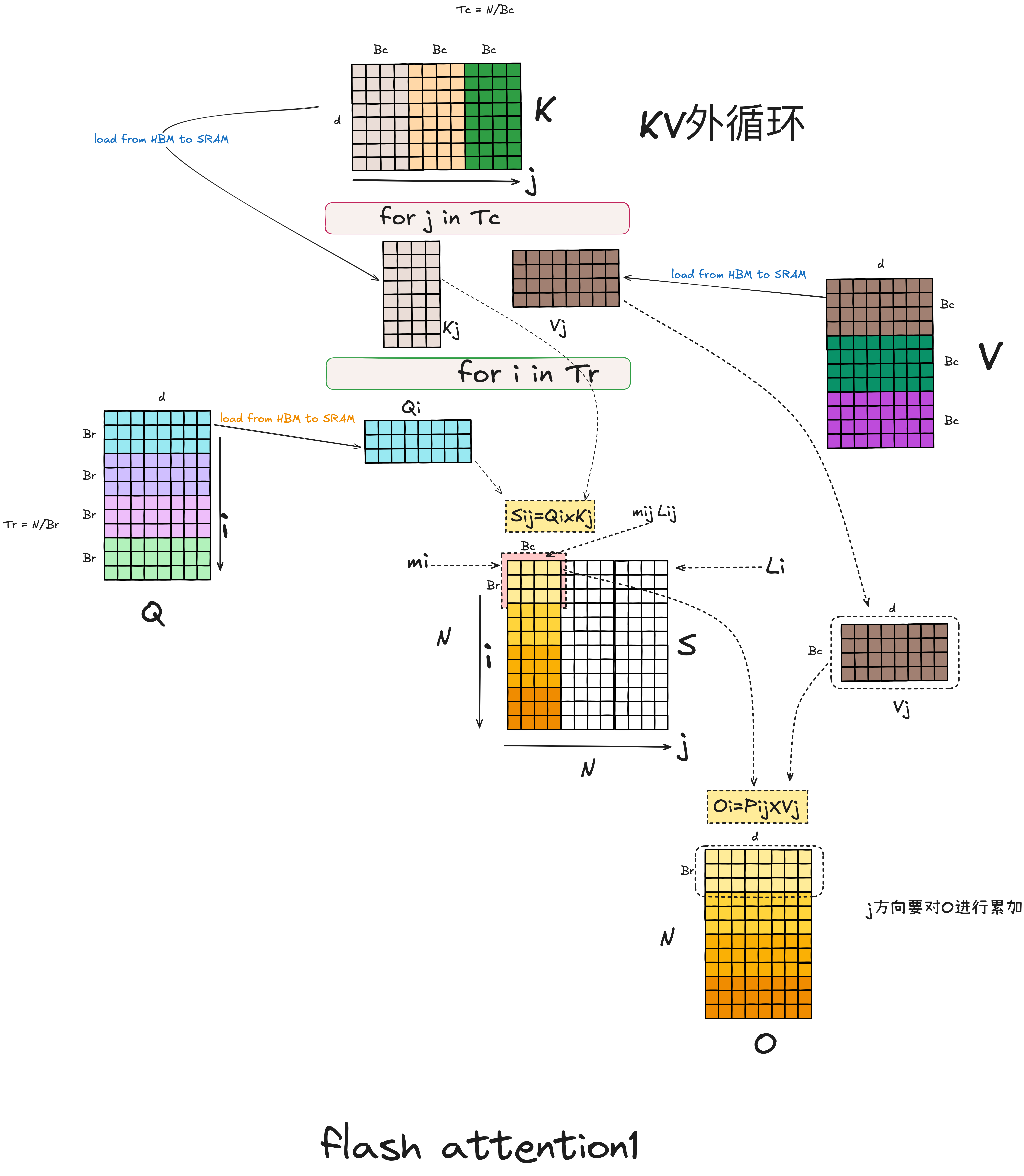
理解了online softmax之后，就可以详细的解释flash attention的算法了。首先对QKV三个矩阵，沿着序列的方向进行分块，外循环是KV矩阵，内循环是Q矩阵，也就是先load KV，然后在当前的KV下，遍历所有的Q去计算。此时在内循环的一个计算中，会计算QK的乘法，然后对这个块矩阵进行online softmax，记录局部\(m\)和局部\(\ell\), 还要计算O，需要注意的是此时计算的O是其中的一部分，每次内循环都需要把之前的O矩阵读入，然后累加，在内循环结束之后一个O的块才被全部计算完成。

Fig. 1. flash-attention1.

复杂度

论文中详细的提到了计算的复杂度的几个计算，下面按照论文中的方式记录一下：

FlashAttention1的FLOPs计算

先看一个循环内，一个循环计算了\(Q\)和\(K\)的乘法，还有和\(V\)的乘法，以及\(softmax\)操作. 其中\(Q_i\)的维度是\(\left[B_r,d\right]\), \(K_{i}^{\top}\)的维度是\(\left[B_c,d\right]\), 因此\(Q_i \times K_{i}^{\top}\)的FLOPs是\(\mathbf{O}(B_rB_cd)\),同理\(V_{i}\)的维度是\(\left[B_c,d\right]\)，\(P_{ij}\)的维度是\(\left[B_r,B_c\right]\),因此\(P_{ij} \times V_{i}\)的FLOPs也是\(\mathbf{O}(B_rB_cd)\)。忽略\(softmax\)的情况下，一个循环内的Flops就是\(\mathbf{O}(B_rB_cd)\)，总共循环的次数是\(T_rT_c=\left\lceil\frac{N}{B_r}\right\rceil \left\lceil\frac{N}{B_c}\right\rceil\),所以总的FLOPs就是：
\[\mathbf{O}(\frac{N^2}{B_rB_c} B_rB_cd) = \mathbf{O}(N^2d)\]
原始的HBM操作次数
1. 对于\(Q,K,V \in \mathbf{R}^{N \times d}\)，计算\(\mathbf{S} = Q K^{\top}\)，会把\(Q\) 和 \(K\) 从HBM载入，把\(S \in \mathbf{R}^{N \times N}\)写出, 因此总共需要\(\mathbf{O}{(Nd+N^2)}\)次HBM读写
2. 对于\(P = softmax(S)\), 需要把\(S\)载入，然后把\(P\)写出，总共需要\(\mathbf{O}{(N^2)}\)次HBM读写
3. 对于\(\mathbf{O} = PV\),需要把\(PV\)载入，把\(O\)写出，总共需要\(\mathbf{O}{(Nd+N^2)}\)次HBM读写
所以整体的HBM的读写次数是\(\mathbf{O}{(Nd+N^2)}\)
FlashAttention1的HBM操作次数
1. 对内循环一次读取1个\(Q_i\)和1个\(O_i\)，同时写出1次\(O_i\)，其中\(Q_i\)和\(O_i\)的大小都是\(B_r \times d\),因此一次内循环读写次数是\(3*B_r \times d\), 总共的内循环此时是\(T_r\)，也就是一次外循环的读写次数是\(3*B_r \times d \times T_r\) = \(\mathbf{O}(N \times d)\)
2. 每次外循环需要载入\(K_i\)和1个\(V_i\),其中\(K_i\)和\(V_i\)的大小都是\(B_c \times d\),总共循环\(T_c\)次，因此总共的读写次数是\(B_c \times d \times T_c\) = \(N \times d\)
3. 总共外循环\(T_c\)次，总共的读写次数是外循环的\(N \times d\)次\(KV\)读写加上 \(T_c \times N \times d\)次内循环的读写，总共\(\mathbf{O}{(N \times d + T_c \times N \times d)}\), 也就是\(\mathbf{O}{(T_c \times N \times d)}\)次
4. \(T_c\)怎么计算？对于SRAM的大小\(M\)，需要满足 \(B_c d = \mathbf{O}(M)\),也就是\(B_c = \mathbf{O}(\frac{M}{d})\) , \(T_c = \frac{N}{B_c} = \frac{Nd}{M}\)
5. 因此FlashAttention1的HBM读写次数是 \(\mathbf{O}{(T_c \times N \times d)}\) = \(\mathbf{O}{(\frac{Nd}{M} \times N \times d)}\) = \(\mathbf{O}{(\frac{N^2d^2}{M})}\)

questions？

在读这个论文的时候有个疑问，就是算法中的分块大小\(B_c=\left\lceil\frac{M}{4 d}\right\rceil, B_r=\min \left(\left\lceil\frac{M}{4 d}\right\rceil, d\right)\) 是怎么推导来的？

一开始的想法是kernel中同时在shared memory存在\(Q,K,V,O,S\)这几个矩阵，假设不考虑\(S\)，那么一共4个矩阵，假设分块大小是\(B\),那么 \(4 \times B \times d \leq M\)就能得到\(B \leq \frac{M}{4d}\)，但这样有点勉强，因为\(M\)是shared memory的大小，是字节数，公式应该是\(4 \times B \times d \times sizeof(dtype) \leq M\),假设是float16推理，那么\(sizeof(float16) = 2\),得到的结果应该是\(B \leq \frac{M}{8d}\)。但无论怎么说都是不精确的，感觉是个经验值，问了deepseek也是说是一个经验值，不是一个严格的数学推导。

FlashAttention2

为什么？

那么FlashAttention2又是解决了什么问题呢？

简单的说就是改进了FlashAttention1能够使Attention计算更快。论文中提到了三个点，最终使Attention快了2到3倍。这三个改进点分别是：

改进FlashAttention1算法，降低FlashAttention1中的非矩阵乘法的计算量
给出如何在不同的线程块上并行计算以充分使用GPU资源
描述了如何将一个线程块中的负载拆分在不同warp之上，以减少共享内存访问的量

下面我们分别介绍。

是什么？

\[\begin{array}{ll} \hline & &\text { Algorithm } 1 \text { FlashAttention-2 forward pass }\\ \hline & &\text { Require: Matrices } \mathbf{Q}, \mathbf{K}, \mathbf{V} \in \mathbb{R}^{N \times d} \text { in HBM, block sizes } B_c, B_r \text {. }\\ &1: &\text { Divide } \mathbf{Q} \text { into } T_r=\left\lceil\frac{N}{B_r}\right\rceil \text { blocks } \mathbf{Q}_1, \ldots, \mathbf{Q}_{T_r} \text { of size } B_r \times d \text { each, and divide } \mathbf{K}, \mathbf{V} \text { in to } T_c=\left\lceil\frac{N}{B_c}\right\rceil \text { blocks } \\ & & \mathbf{K}_1, \ldots, \mathbf{K}_{T_c} \text { and } \mathbf{V}_1, \ldots, \mathbf{V}_{T_c} \text {, of size } B_c \times d \text { each. }\\ &2: &\text { Divide the output } \mathbf{O} \in \mathbb{R}^{N \times d} \text { into } T_r \text { blocks } \mathbf{O}_i, \ldots, \mathbf{O}_{T_r} \text { of size } B_r \times d \text { each, and divide the logsumexp } L \\ & & \text { into } T_r \text { blocks } L_i, \ldots, L_{T_r} \text { of size } B_r \text { each. }\\ &3: &\text { for } 1 \leq i \leq T_r \text { do }\\ &4: & \quad \text { Load } \mathbf{Q}_i \text { from HBM to on-chip SRAM. }\\ &5: & \quad \text { On chip, initialize } \mathbf{O}_i^{(0)}=(0)_{B_r \times d} \in \mathbb{R}^{B_r \times d}, \ell_i^{(0)}=(0)_{B_r} \in \mathbb{R}^{B_r}, m_i^{(0)}=(-\infty)_{B_r} \in \mathbb{R}^{B_r} \text {. }\\ &6: &\quad \text { for } 1 \leq j \leq T_c \text { do }\\ &7: &\qquad \text { Load } \mathbf{K}_j, \mathbf{V}_j \text { from HBM to on-chip SRAM. }\\ &8: &\qquad \text { On chip, compute } \mathbf{S}_i^{(j)}=\mathbf{Q}_i \mathbf{K}_j^T \in \mathbb{R}^{B_r \times B_c} \text {. }\\ &9: &\qquad \text { On chip, compute } m_i^{(j)}=\max \left(m_i^{(j-1)}, \operatorname{rowmax}\left(\mathbf{S}_i^{(j)}\right)\right) \in \mathbb{R}^{B_r}, \tilde{\mathbf{P}}_i^{(j)}=\exp \left(\mathbf{S}_i^{(j)}-m_i^{(j)}\right) \in \mathbb{R}^{B_r \times B_c} \\ & &\qquad \text { (pointwise), } \ell_i^{(j)}=e^{m_i^{j-1}-m_i^{(j)}} \ell_i^{(j-1)}+\operatorname{rowsum}\left(\tilde{\mathbf{P}}_i^{(j)}\right) \in \mathbb{R}^{B_r} \text {. }\\ &10: &\qquad \text { On chip, compute } \mathbf{O}_i^{(j)}=\operatorname{diag}\left(e^{m_i^{(j-1)}-m_i^{(j)}}\right) \mathbf{O}_i^{(j-1)}+\tilde{\mathbf{P}}_i^{(j)} \mathbf{V}_j \text {. }\\ &11: &\quad \text { end for }\\ &12: &\quad \text { On chip, compute } \mathbf{O}_i=\operatorname{diag}\left(\ell_i^{\left(T_c\right)}\right)^{-1} \mathbf{O}_i^{\left(T_c\right)} \text {. }\\ &13: &\quad \text { On chip, compute } L_i=m_i^{\left(T_c\right)}+\log \left(\ell_i^{\left(T_c\right)}\right) \text {. }\\ &14: &\quad \text { Write } \mathbf{O}_i \text { to HBM as the } i \text {-th block of } \mathbf{O} \text {. }\\ &15: &\quad \text { Write } L_i \text { to HBM as the } i \text {-th block of } L \text {. }\\ &16: &\text { end for }\\ &17: &\text { Return the output } \mathbf{O} \text { and the logsumexp } L \text {. } \\ \hline \end{array}\]

这个就是FlashAttention2的算法部分(我们这里只关注前向)，我们下面详细介绍一下具体的改进。

怎么做？

对FlashAttention1算法的改进

FlashAttention2对FlashAttention1的改进主要在非矩阵乘法的部分，意思是不需要存储临时的\((m{(x)},\ell{(x)})\)。根据之前推导过的online softmaxsee From Online Softmax to FlashAttention , 我们可以知道：

\[\begin{aligned} m^{(1)} & =\operatorname{rowmax}\left(\mathbf{S}^{(1)}\right) \in \mathbb{R}^{B_r} \\ \ell^{(1)} & =\operatorname{rowsum}\left(e^{\mathbf{S}^{(1)}-m^{(1)}}\right) \in \mathbb{R}^{B_r} \\ \tilde{\mathbf{O}^{(1)}} & =e^{\mathbf{S}^{(1)}-m^{(1)}} \mathbf{V}^{(1)} \in \mathbb{R}^{B_r \times d} \\ m^{(2)} & =\max \left(m^{(1)}, \operatorname{rowmax}\left(\mathbf{S}^{(2)}\right)\right)=m \\ \ell^{(2)} & =e^{m^{(1)}-m^{(2)}} \ell^{(1)}+\operatorname{rowsum}\left(e^{\mathbf{S}^{(2)}-m^{(2)}}\right)=\operatorname{rowsum}\left(e^{\mathbf{S}^{(1)}-m}\right)+\operatorname{rowsum}\left(e^{\mathbf{S}^{(2)}-m}\right)=\ell \\ \tilde{\mathbf{P}}^{(2)} & =\operatorname{diag}\left(\ell^{(2)}\right)^{-1} e^{\mathbf{S}^{(2)}-m^{(2)}} \\ \tilde{\mathbf{O}}^{(2)} & =\operatorname{diag}\left(e^{m^{(1)}-m^{(2)}}\right) \tilde{\mathbf{O}}^{(1)}+e^{\mathbf{S}^{(2)}-m^{(2)}} \mathbf{V}^{(2)}=e^{s^{(1)}-m} \mathbf{V}^{(1)}+e^{s^{(2)}-m} \mathbf{V}^{(2)} \\ \mathbf{O}^{(2)} & =\operatorname{diag}\left(\ell^{(2)}\right)^{-1} \tilde{\mathbf{O}}^{(2)}=\mathbf{O} . \end{aligned}\]

也就是说根本不需要记录\((m{(x)},\ell{(x)})\)，在一次循环中就可以解决，如果要这样做，就需要循环的时候按输出矩阵的行计算，也就是，相比FlashAttention1来说，由KV作为外循环变成由Q变成外循环，这样的更改的意思是，在一次循环\(Q\)的时候，就可以计算一行输出矩阵，这样也同时减少了对输出矩阵\(\mathbf{O}\)的多次读写。流程图如下：

Fig. 2. flash-attention2.

也就是说对于FlashAttention2的前向计算来说，主要的更改就是更改了\(Q\)和\(K,V\)的循环顺序，这样的更改可以更好的利用online softmax的特性，不需要存储\((m{(x)},\ell{(x)})\)，也不需要多次读写\(\mathbf{O}\)矩阵。

并行

这个更改点是指在FlashAttention1上并行的时候是对batch 和 num_heads维度进行并行，但这样对SM的利用率不高，FlashAttention2中改成了对batch 和 num_heads维度还有seq维度进行并行，增加了SM利用率。

Work Partitioning Between Warps

FlashAttention2将Q分成4个warp，同时使所有warp都可以访问K和V。在每个warp执行矩阵乘以获得\(QK\)的矩阵之后，他们只需要乘以共享\(V\)即可获得相应的输出对应的块。warp之间不需要通信，因此会减少共享内存读取/写入进而产生加速。

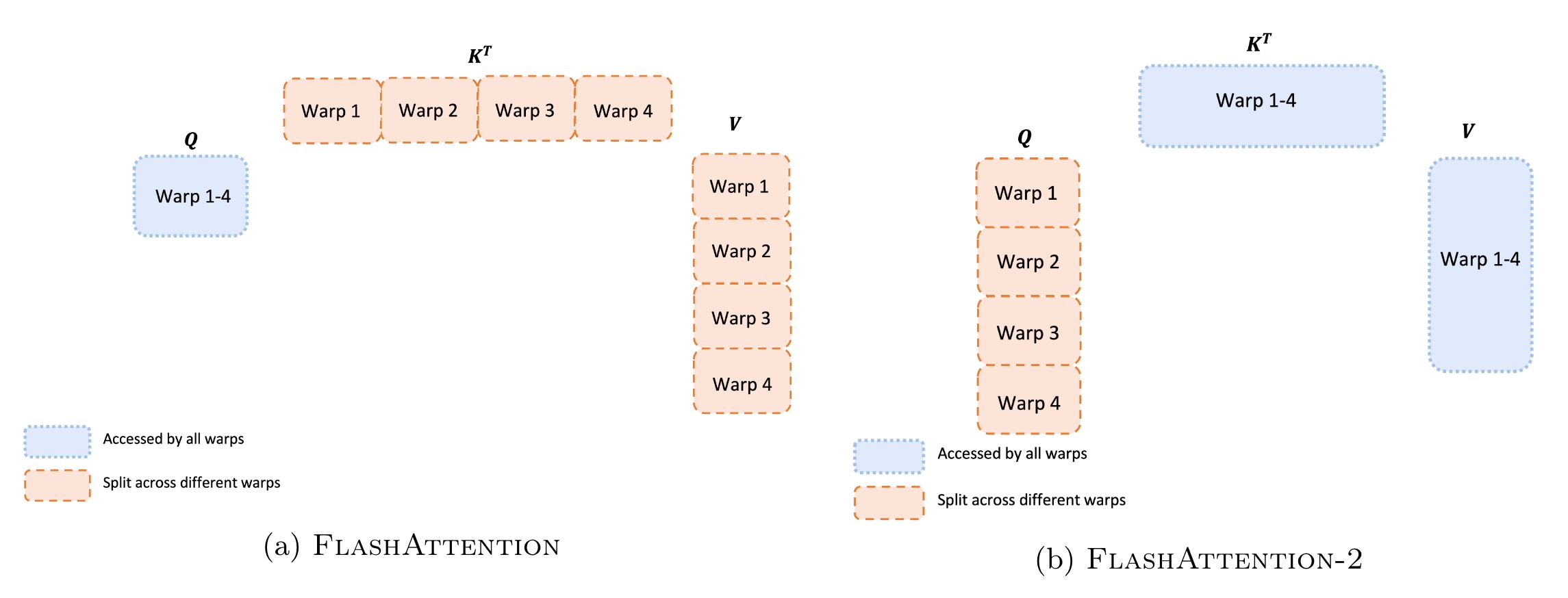
Fig. 3. warps between flash attention1 and flash attention2.

这个部分对我来说，一开始是完全不明白的。后来明白，对于这个其实就是对应的你是如何去抛thread block的，把\(QK\)分成4个warp也就是每个warp都只加载需要计算的那部分的\(QK\)块，\(KV\)则是对所有warp都共享的，实际上我理解可以对应算法中的内外循环的不同。

FlashAttention3

对于FlashAttention3没有完全研究明白，下面的内容照搬：这里

为什么？

FlashAttention3 解决了什么问题？简单的说是在H100之上做了一些基于硬件特性的性能优化，解决了FlashAttention2在H100上对GPU利用率低这个问题。在 A100 上相比于传统的非融合 Attention， FlashAttention2实现了 2-4x 的提速，GPU 利用率在 80%-90% 之间。然而 FlashAttention2 在 H100 上的利用率不高，仅有 35% 左右。

H100 新增了 TMATensor Memory Accelerator, see Nvidia TensorCore for details 硬件、 Warpgroup 级别的 GEMM 指令，是 NV 首个可实现完全异步通信和计算的 GPU，同时具有 FP8 低精度运算的能力。FA2 尚未利用 Hopper 架构的新特性、异步通信计算、低精度运算带来的性能提升，因此吞吐无法在现代架构上实现最大化。

是什么？

H100架构特性

WGMMA(Warpgroup MMA)

Warpgroup 指的是 4 个连续的 warps，共 128 个连续的 threads，正好对应了一个 SM 最多可并行计算的线程数。在 H100 上，我们可以以 Warpgroup 为粒度调度 GEMM 运算。下面说明了 A100 和 H100 调度 GEMM 的 API 的区别：

A100上，wmma.mma.sync (warp-level) 和 mma.sync(thread-level) 均为调用 Tensor Core 计算的同步 API，也就是必须等到结果计算出来，线程才能继续执行下一个指令；
H100上，新增的 wgmma.mma_async(warpgroup-level) 可以异步运行 Tensor Core，也就是可以与其他单元并行计算（例如 CUDA Core）。WGMMA operand A 可以从 RMEM/SMEM 读取，operand B 只能从 SMEM 读取。

在 FA3 论文的算法中将 GEMM 分为两类，其中 RS-GEMM 表示 operand A 在 RMEM 上,operand B 在 SMEM 上，SS-GEMM 表示 operand A, B 均在 SMEM 上。see cuda Doc for details

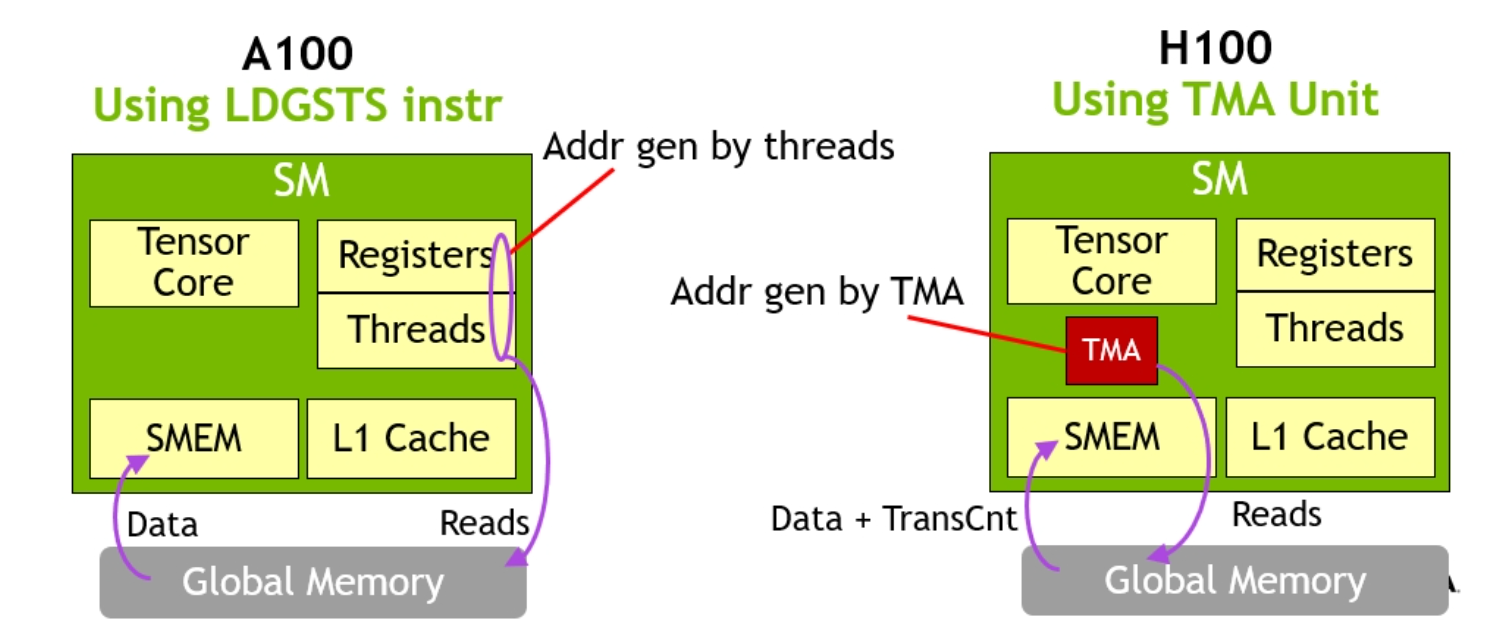
TMA

TMA 是 H100 新增的硬件单元，它允许程序在 GMEM 和 SMEM 之间异步且双向地传输 1D 到 5D 的张量。通过这个专门用于数据移动的硬件单元，线程可以被解放出来做其他工作，而不是计算地址和管理数据移动，这消除了 Hopper 架构之前 SM 必须使用寄存器在不同内存空间之间移动数据的需求。

TMA 指令非常轻量化，只需要一个线程即可启动 TMA 传输。

Fig. 4. TMA.

FP8 低精度运算

H100 支持FP8低精度运算。

怎么做？

1. overlap overall computation and data movement via warp-specialization

在 Hopper 架构下，我们可以充分利用 Warp Specialization + Intra-warpgroup overlapping 的异步性，实现计算与通信、计算与计算之间的 overlap。

A100 之前的异步：Warp Specialization。Warp Specialization 的目标是掩盖通信延迟，让计算单元（如 CUDA Core / Tensor Core）尽可能满载运行。具体做法是往 SM 里塞尽可能多的 warps，通过 SM 中的 warp schedulers 在不同的 warp 间切换实现异步。例如，如果一个 warp 正在等待数据，可以切换成另一个 warp 进行计算。由于所有 warp 中所有的线程均保存在 register file 中，warp 的上下文切换是几乎没有成本的，在一个时钟周期里就可以完成。

一般而言，我们会指定一些 warp 进行数据传输（producer），另一些 warp 读取数据进行计算（consumer），两者通过 barrier 进行数据依赖的同步。通过 warp scheduler 的调度，数据复制的延时就可以很好地被计算所隐藏，反之亦然

A100 的异步：Multistage。A100 新增的cp.async指令，可以在同一 warp 中实现前一块数据的计算和后一块数据通信的 overlap，因此就能通过编排流水线的方式实现异步，这就是 Multistage。由于在 warp 内部实现了异步，采用 warp 间异步的 warp specialization 便不再需要。Multistage 也是 FA2 的工程实现方式。

由于 warp 需要保留当前计算的数据以及预留后面传输过来的数据，通常 warp 要保留至少 2 份数据缓存空间，即 double buffer。如果 stage 数量进一步增加，就需要保留更多的 buffer。

H100 的异步：Warp Specialization + Intra-warpgroup overlapping。一方面，由于 TMA 在硬件上实现了数据传输的异步，我们不再需要 Multistage 那样由 warp 自行处理数据传输了。另一方面，由于 WGMMA 指令的出现，从 warpgroup 维度调度线程能够享受 WGMMA 的异步性。同时 1）Hopper 架构新增了在不同 warpgroup 间重新分配寄存器（warpgroup-wide register reallocation）的 API setmaxnreg；2）TMA 仅需一个线程发送指令即可运行。我们可以给 producer 分配最少的资源，consumer 分配更多的资源，从而最大化有效算力。因此 Warp Specialization 方案能够提供更快的运算速度。

同时，在 consumer warpgroup 内部，我们仍然可以采用 GEMM 和 softmax 的 overlap 来实现两个 warpgroup 计算和计算的同时进行，也就是 Intra-warpgroup overlapping。这就是 FA3 采用的异步策略。

由于 H100 的 Tensor Core 运算速度更快，我们需要更极致的异步来掩盖通信延时，因此结合 Warp Specialization 和 Intra-warpgroup overlapping 的优势便能够实现 FA3 快速的运算。

我们用一张图简单说明 Warp Specialization、Multistage，以及将 Warp Specialization 和 Multistage 的思想结合，变为 Ping-Pong Scheduling 这三者的区别：

Fig. 5. 三种异步的比较.

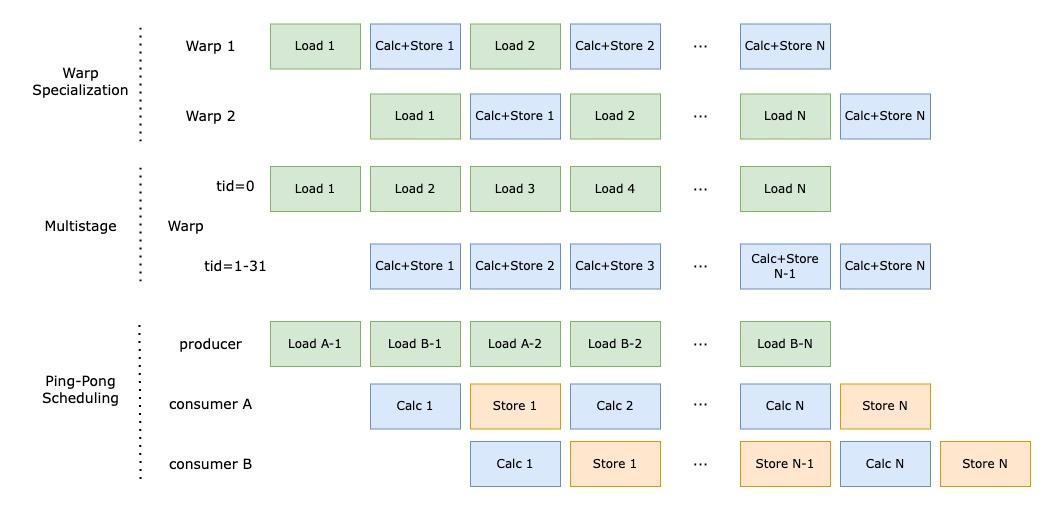
我们结合以下的流程图，从微观层面介绍 Warp Specialization 单个 SM 中 Producer 和 Consumer 是如何进行协作和实现异步性的。

Fig. 6. Producer 和 Consumer 的异步.

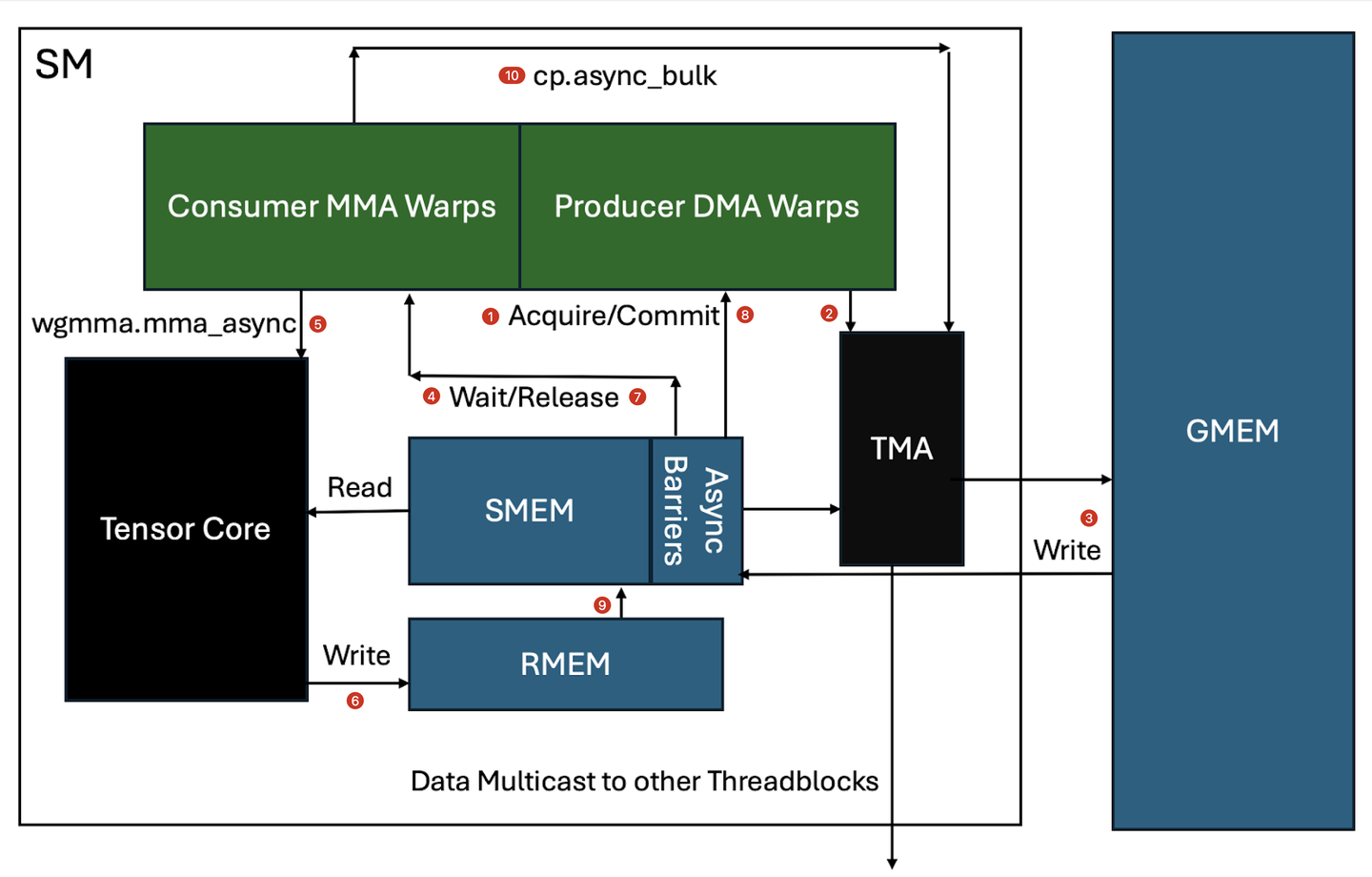
producer warpgroup 获取 SMEM 缓冲区的 barrier lock。
producer warpgroup 通过单个线程向 TMA 芯片发起 TMA 请求。
TMA 计算所需的实际 SMEM 地址，将数据移动到 SMEM，并在移动时会进行数据布局转换（如 swizzling），以便在 SMEM 中实现最快速（无 bank conflict）的访问。数据也可以 multicast 到其他 SM，或者可能需要等待来自其他 TMA multicast 的数据以完成加载。（thread block cluster 可以在多个 SM 之间共享 SMEM）
此时，barrier 被更新以信号通知数据已到达 SMEM。
相关的 consumer warpgroup 现在开始工作，发出多个 wgmma.mma_async 命令，这些命令将数据从 SMEM 读取到 Tensor Core，随后进行矩阵乘法计算。
MMA 累加后的值在完成计算后被写入 RMEM。
consumer warpgroup 释放 SMEM 上的 barrier。
producer warpgroup 开始工作，发出下一条 TMA 指令以重新填充现在空闲的 SMEM 缓冲区。
consumer warpgroup 同时对累加结果进行后处理（epilogue），然后将数据从 RMEM 移动到不同的 SMEM 缓冲区。
consumer warpgroup 发出 cp.async_bulk 命令，将数据从 SMEM 移动到 GMEM。

从宏观层面看，为最大化提升性能，我们希望一个 SM 仅占有一个 thread block，这个 block 中的 warpgroup 由多个 Producer 和多个 Consumer 组成。下面以 1 Producer + 2 Consumers 为例。

Fig. 7. Ping-Pong Architecture

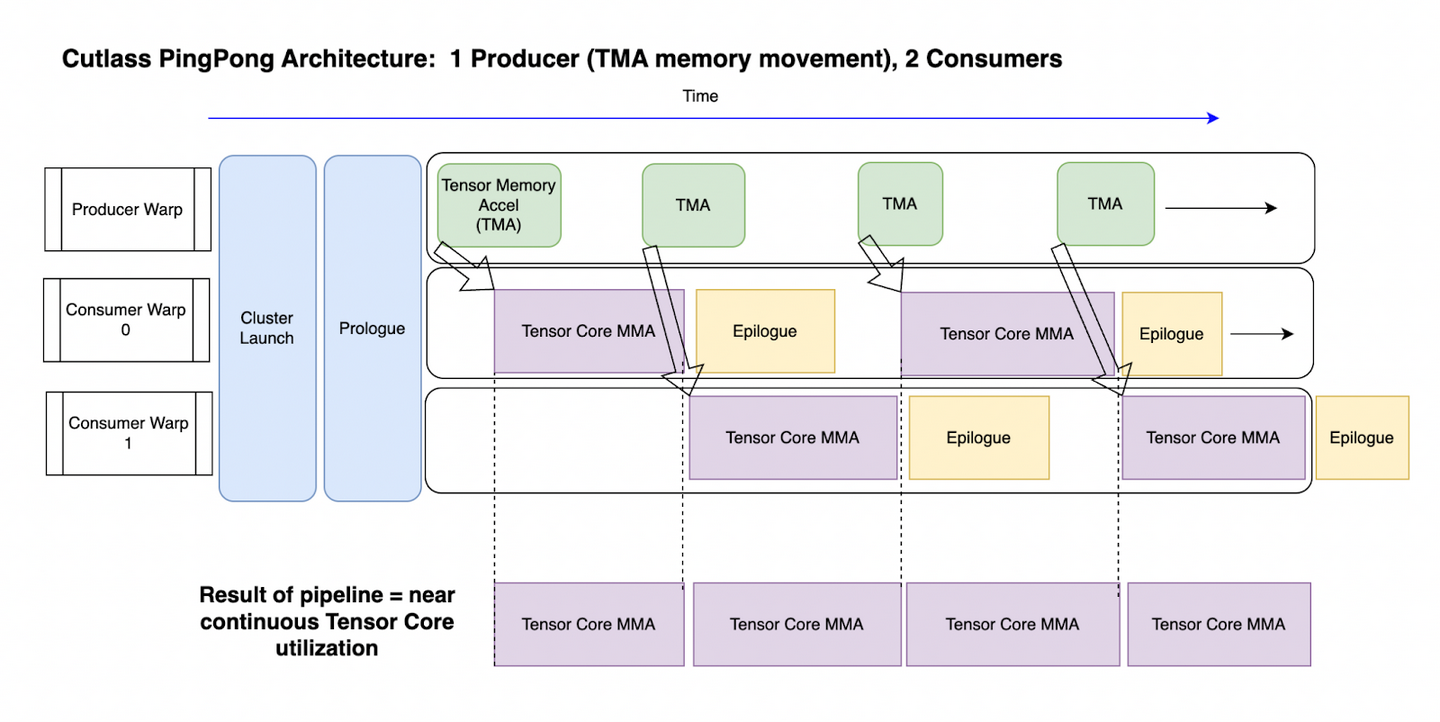
Producer： warpgroup 中每个线程分配 24 个 registers，主要职责是分发 TMA 指令，由 TMA 将数据从 GMEM 移至 SMEM。数据传输完成后，TMA 会通知相应的 consumer 数据已准备就绪。Producer 会推举出一个 leader 线程发送 TMA 异步指令，指令结束后即停止运行，等待 SMEM buffer 释放；
Consumers：每个 warpgroup 的线程分配 240 个 registers，主要职责是获取 SMEM buffer 的数据，计算 GEMM 和 softmax，释放 buffer 并通知 producer 数据已被释放。随后处理收尾的计算任务、计算结果的数据传输等工作，这也被称为 epilogue 阶段。

这里寄存器的分配个数是通过setmaxnreg 指定的。寄存器分配需要满足一系列的约束条件：

setmaxnreg可指定特定 warpgroup 每个线程所分配到的寄存器数量。这个数量必须在 [24, 256] 之间，且必须为 8 的倍数；每个 warpgroup 的每个线程分配的寄存器不超过 255 个（CUDA/NVCC 限制）；

每个线程所在的所有 warpgroup 分配的寄存器总和不超过 512 个（因为一个 SM 内总共有 64k 个寄存器，一个 warpgroup 包含 128 个线程，所以每个线程只能保留 64k/128 = 512 个寄存器。在我们的例子中，每个线程都位于 1 Producer + 2 Consumers 中，因此寄存器数量为 24 + 240 + 240 = 504 < 512）；

每个线程所在的所有 warpgroup 分配的寄存器总和必须为 warpgroup 数量的整数倍（例如这里有 3 个 warpgroup，那么 24/240/240 共 504 个寄存器恰好是 3 的倍数，而 32/240/240 即使符合上面的三个条件，但总和 512 并非为 3 的倍数，因此不成立）。为尽可能减少 Producer 的寄存器，增加 consumer 的寄存器，24/240/240 就是 1 Producer + 2 Consumers 的最佳分配方案。对于 1 Producer + 3 Consumers 而言，32/160/160/160 也是最佳的分配方案。

Producer 和 Consumers 之间的通信机制是依靠 CUTLASS 的 Asynchronous Pipeline Class + Barriers 来实现的。

对于Ping-pong scheduling 主要发生在两个 consumer warpgroup 之间。由于 WGMMA 的异步性，我们可以同时运行 softmax 和 GEMM 计算，按照下图的调度并用bar.sync在虚线处同步，可以让两个 warpgroup 轮流交替进行 GEMM 计算，以实现更高的 Tensor Core 算力利用率。

Fig. 8. Ping-Pong Scheduling

2. interleave block-wise matmul and softmax operations

在同一个 warpgroup 内部，也可以按照下图编排流水线的方式，实现 GEMM 和 softmax 的计算重叠。下图展示的是 2-stage 流水线方案。

Fig. 9. Intra-warpgroup overlap

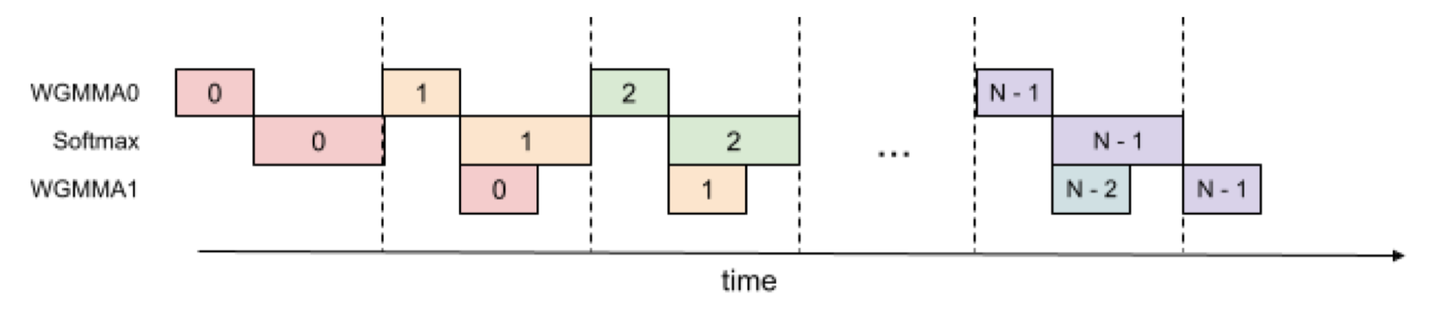
注意，在 2-stage 方案中，寄存器需要同时保存前一份数据 softmax 的计算结果和后一份数据 GEMM0 的计算结果，因此寄存器的压力会比没有流水线的情况要大。

理论上，三个计算步骤可以安排 3-stage 流水线，但由于寄存器数量的限制，强行编排三级流水线，要么会造成寄存器溢出，极大程度影响性能，要么只能选择更小 block size，同样会影响性能。FA3 经性能测试后，采用了 2-stage 的方案。

3. block quantization and incoherent processing that leverages hardware support for FP8 low-precision.

量化

FA3 在转换 FP8 时做了 Block-wise 的量化，由于 FA3 计算就是按照一个一个 Block 运算的，所以无论是量化和反量化的操作都非常简单，计算量也非常少。

此外，FA3 在对 GEMM 运算量化前，对两个矩阵操作数 A, B 均乘上一个随机的正交矩阵 M，这样数学上矩阵的结果不变，但可以减少量化前 A, B 矩阵的 outliers，进而减少量化损失。实际上，论文中的 M 是通过一个随机的只包含 {-1, 1} 的对角矩阵乘上一个 Hadamard 矩阵来生成一个随机的正交矩阵的，这个生成的计算复杂度可以从 \(O(d^2)\) 降低至 \(O(d log d)\)，而且可以与 RoPE 运算相融合且不增加额外的计算量。