Attention系列整理Part1-基础

Created on April 03, 2025

2025   ·   attention   ·   AI

Attention是整个Transformer的基础，因此想着全面的梳理一下Attention的相关的知识，主要从基础理论和计算方面着手，然后会继续分析现有的FlashAttention的详细计算等等。

为什么？

最早开始接触Attention是在《Attention is all your need》这篇文章中，但实际上Attention的机制早就出现且在NLP中应用。在某种程度上，Attention是受我们如何将视觉注意力放在图像的不同区域或如何将一个句子中的单词关联起来启发的，就像人类视觉一样，注意力使我们能够以“高分辨率”聚焦于某个区域（例如，查看黄色框中的尖耳朵），同时以“低分辨率”感知周围的图像（例如，现在雪景背景和服装怎么样？），然后调整焦点或进行相应的推理Attention? Attention! 。

Fig. 1. A Shiba Inu in a men’s outfit. The credit of the original photo goes to Instagram @mensweardog.


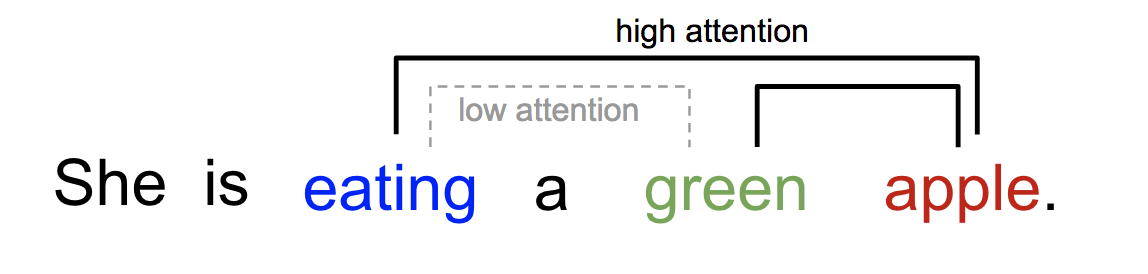
类似的，我们可以在一个句子或密切上下文中解释单词之间的关系。当我们看到“eating”时，我们期望很快就会遇到一个描述食物的词。虽然颜色也描述了食物，但可能与“eating”不太直接相关。

Attention 机制最早在 Seq2Seq（Sequence-to-Sequence）模型中被提出，其主要目的是克服 RNN 在长序列处理中的瓶颈，之后在 Transformer中被广泛应用，并彻底改变了自然语言处理（NLP）和计算机视觉（CV）领域的模型架构。

Attention主要解决的问题是:

  • 信息瓶颈问题（Information Bottleneck）

传统的编码器-解码器架构（如RNN）将整个输入序列压缩为一个固定长度的上下文向量。当处理长序列时，这一向量难以完整保留所有信息，导致信息丢失。注意力机制允许解码器在生成每个输出时动态访问输入序列的全部隐藏状态，而非依赖单一固定向量，从而缓解信息压缩的局限性。

  • 长距离依赖建模（Long-range Dependencies）

RNN/LSTM在处理长序列时，早期输入的信息可能因逐层传递而逐渐稀释，难以捕捉远距离词之间的关系。 注意力机制通过直接计算输入序列中任意两个位置的相关性（如自注意力），模型能够高效捕捉全局依赖，无论词之间的距离远近。

更多更详细的Attention发展历程参考Lil’Log: Attention? Attention!

是什么？

Fig. 2. Attention in transformer.

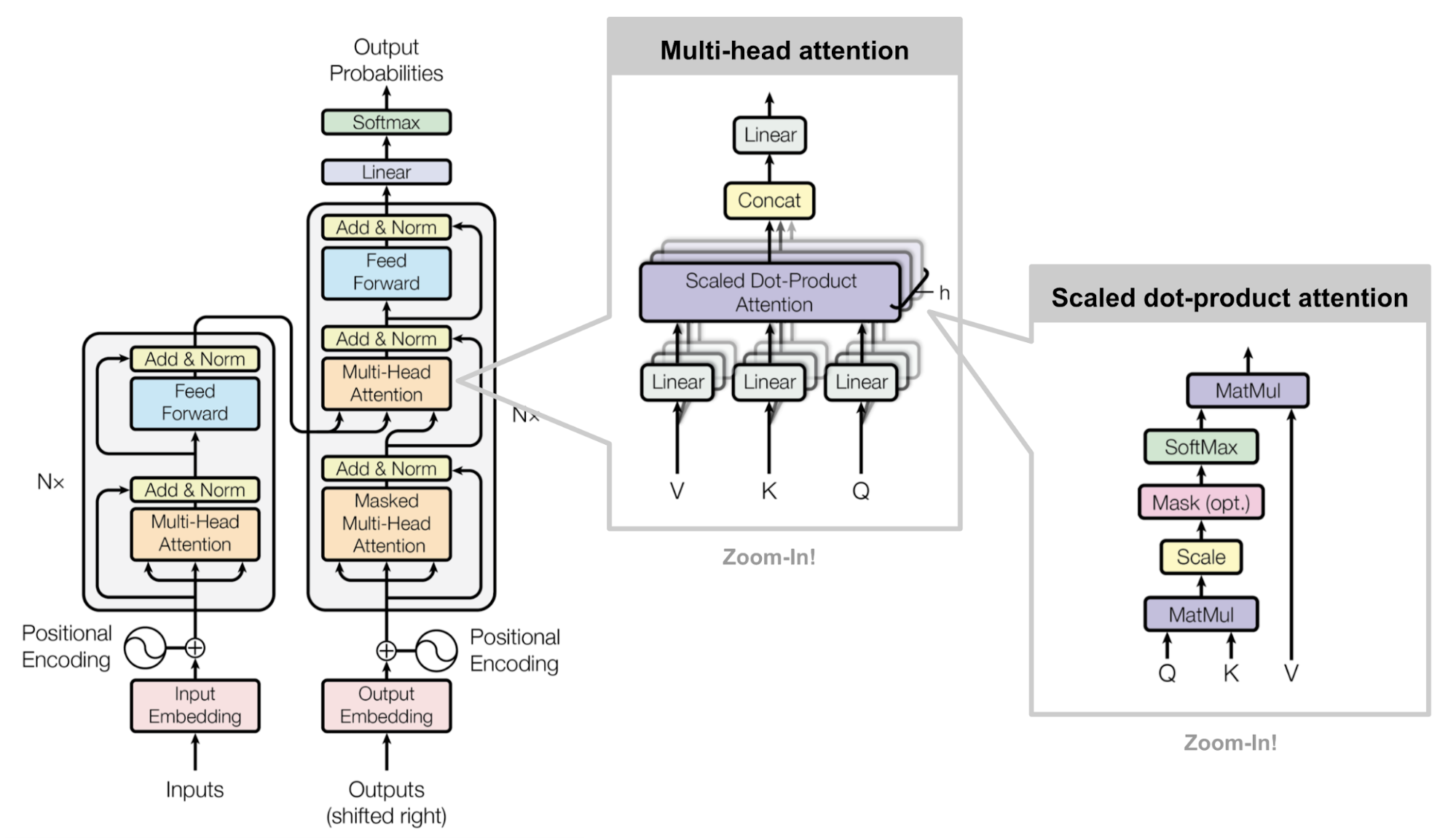
Transformer模型对注意力机制进行了形式化定义：注意力机制可以被描述为一个函数，该函数将一个查询（query，简写为 \(Q\) ）和一个具有 \(M\) 个元素的键－值（key－value，分别简写为 \(K\) 和 \(V\) ）集合（这个键－值集合也称之为＂source＂，即＂源＂）映射为一个值（value）。该函数可以表示为 \(attention ：\left(Q,\left\{k_i, v_i\right\}_M\right) \rightarrow V\) 。在具体计算时，注意力的计算分为三个步骤：

  • 第一步，用输入的 $Q$ 与集合 \(\left\{k_i, v_i\right\}_M\) 中的每一个 \(k_i(i=1,2, \ldots, M)\) 计算相似度，得到 \(M\) 个相似度；

  • 第二步，通过 softmax 函数将 \(M\) 个相似度进行概率化，该步骤会得到一个 \(M\) 维概率分布；

  • 第三步，用概率化后的相似度作为权重系数，对集合 \(\left\{k_i, v_i\right\}_M\) 中的 \(\left\{v_i\right\}\) 做加权求和，得到最终的输出 \(V\) 。上述注意力机制的形式化表达为

\begin{equation} \label{eq:1} \begin{aligned} & \operatorname{similarly} (Q,\lbrace k_i, v_i \rbrace _M) = [ \operatorname{similarly} (Q, k_1), \dots, \operatorname{similarly} (Q, k_M) ] \end{aligned} \end{equation}

\begin{equation} \label{eq:2} \begin{aligned} & [p_1, \cdots, p_M]=\operatorname{softmax}(Q,\lbrace{k_i, v_i\rbrace}_M) \end{aligned} \end{equation}

\begin{equation} \label{eq:3} V = \operatorname{attention}\left(Q,\lbrace{ k_i, v_i \rbrace}_M\right) = \sum_{i=1}^M p_i v_i \end{equation}

上式中， \(\operatorname{similarly}(\cdot, \cdot)\) 为相似度函数，一种最简单的实现形式即为对输入的两个向量计算点积 （dot-product）（注：也可以使用夹角余弦甚至是基于神经网络的相似性度量方法）。从机制上看，注意力机制聚焦的过程体现在权重系数上，权重越大表示投射更多的注意力在对应的值上，即权重代表了信息的重要性。


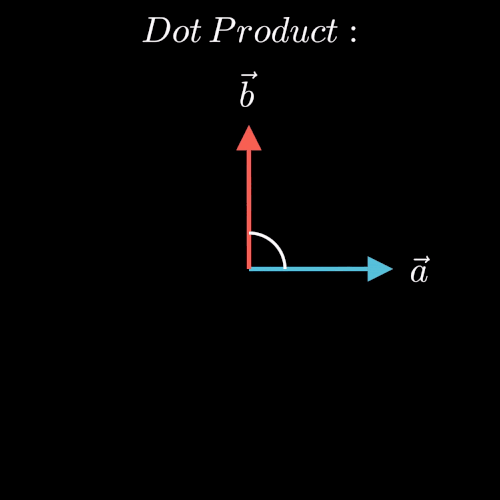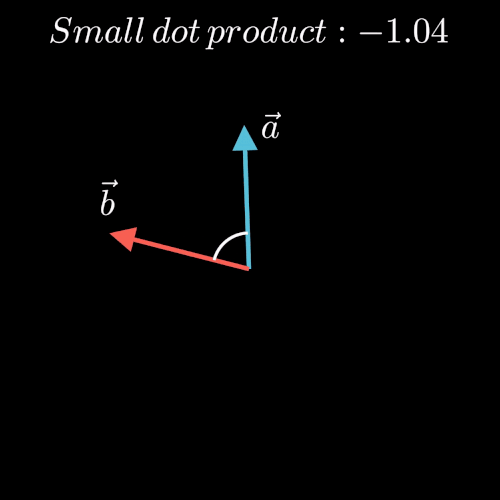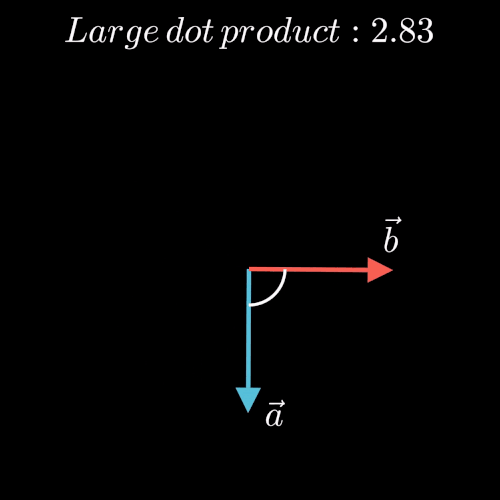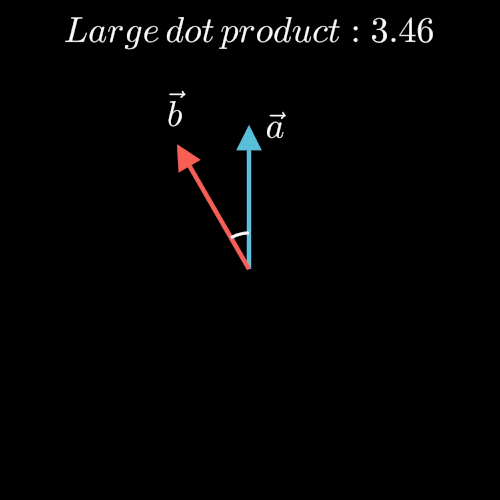
点积表示两个向量在方向上的相似度，值越大越相似，也就是夹角越小。(图片来源于博客)


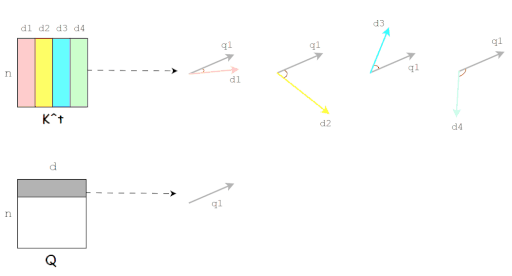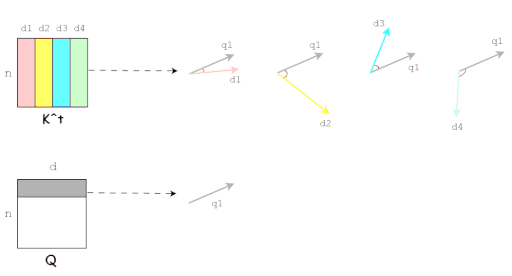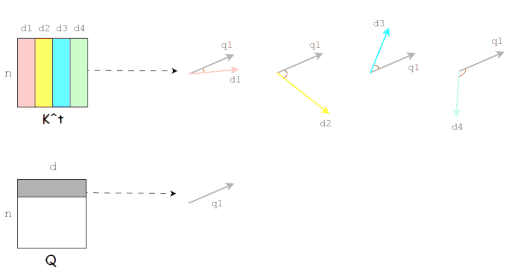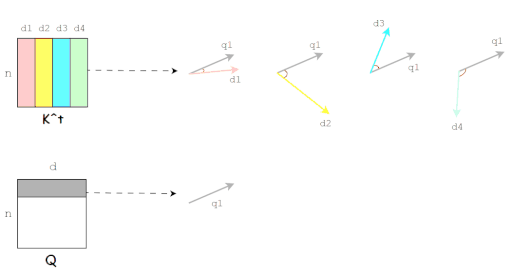
Q和K的内积也就是Q和K的相似性度量。(图片来源于博客)

在《Attention is all your need》这篇文章中介绍了两个Attention，一个是Scale Dot Product Attention, 一个是Multi-Head Attention.

Fig. 3. Attentions.

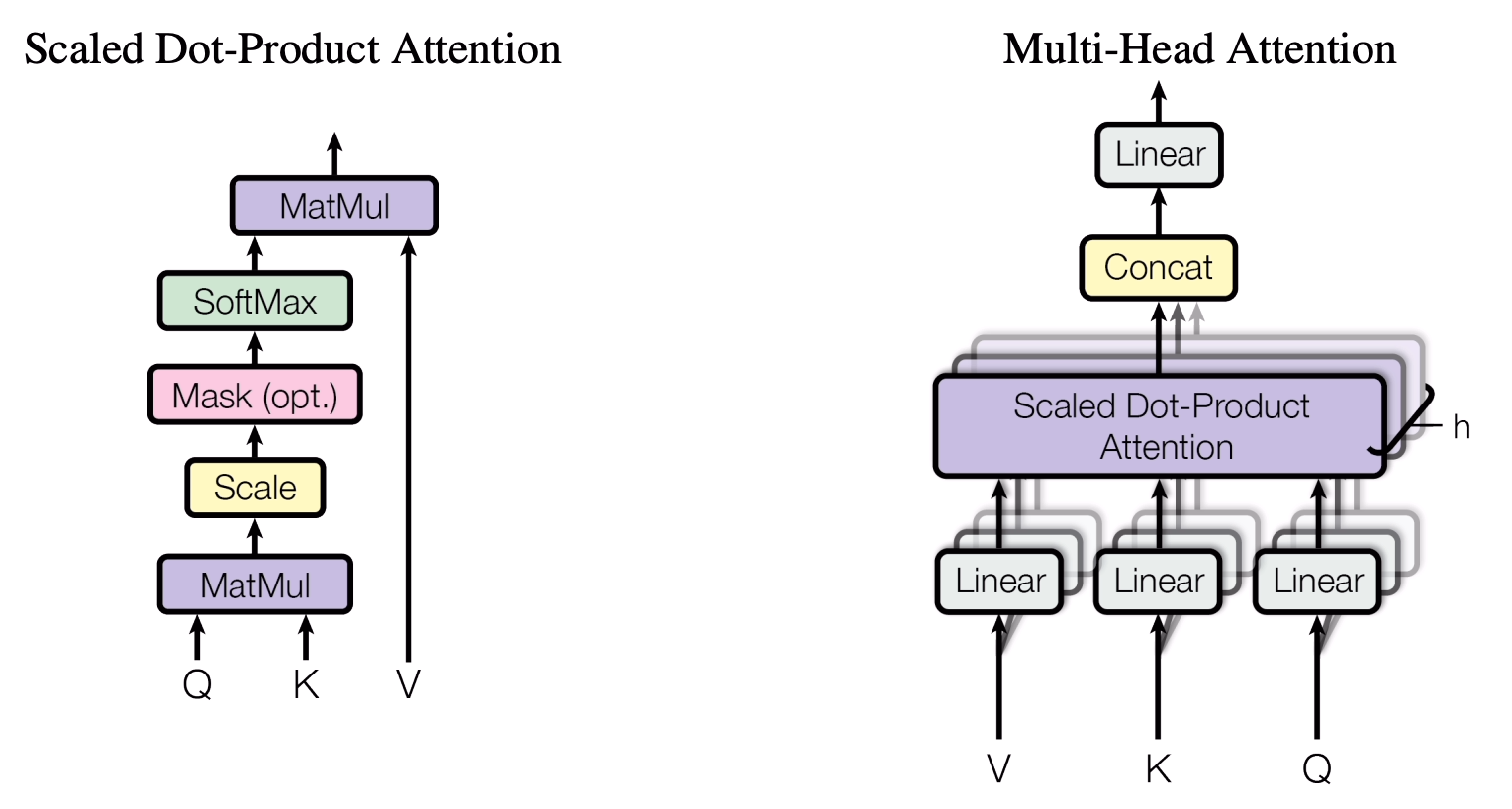
Scale Dot Product Attention

SDPA的公式如下：

\begin{equation} \label{eq:4} \begin{aligned} Attention(Q,K,V) = softmax(\frac{QK^T}{\sqrt{d_k}}) V \end{aligned} \end{equation}

实际上就是之前介绍的注意力的直接表达。 要注意的是这里的相似度量采用的是内积。根据论文中的介绍，最常用的两种注意力函数是加法注意力和点积（乘法）注意力。除了 \(\frac{1}{\sqrt{d_k}}\) 这里的\(d_k\)表示的是输入\(K\)的维度 的缩放因子外，点积注意力与SDPA算法相同。加法注意力使用具有单个隐藏层的前馈网络计算兼容性函数。虽然两者在理论复杂度上相似，但点积注意力在实践中更快、更节省空间，因为它可以使用高度优化的矩阵乘法代码来实现。虽然对于较小的 \(d_k\) 值，这两种机制的表现相似，但对于较大的 \(d_k\) 值，加法注意力优于没有缩放的点积注意力。原因可能是对于较大的\(d_k\) 值，点积的结果值会变大，从而将 softmax 函数推入具有极小梯度的区域。为了抵消这种影响，将点积注意力引入缩放因子\(\frac{1}{\sqrt{d_k}}\) 。

Multi-Head Attention

多头注意力机制，实际上是为了解决单一的Attention表达能力受限的问题，多头注意力将输入通过多个线性变换投影到不同的子空间，每个头都独立执行Attention操作，从多个视角学习信息（例如，一个头可能关注语法结构，另一个关注语义关系）。具体的表达如下：

\[\begin{aligned} \operatorname{MultiHead}(Q, K, V) & =\operatorname{Concat}\left(\operatorname{head}_1, \ldots, \operatorname{head}_{\mathrm{h}}\right) W^O \end{aligned}\]

\begin{equation} \label{eq:5} \begin{aligned} \text { where head } =\operatorname{Attention}\left(Q W_i^Q, K W_i^K, V W_i^V\right) \end{aligned} \end{equation}

其中的参数矩阵 $W_i^Q \in \mathbb{R}^{d_{\text {model }} \times d_k}, W_i^K \in \mathbb{R}^{d_{\text {model }} \times d_k}, W_i^V \in \mathbb{R}^{d_{\text {model }} \times d_v}$ and $W^O \in \mathbb{R}^{h d_v \times d_{\text {model }}}$这里的\(d_{model} = d_k * h(num\_heads)\)。\(d_k\) 和 \(d_v\) 一般是相同的 .

attention 变种

除了上述两种Attention，还有一些Attention的变种，分别介绍一下：

self-attention

self-attention即自注意力，意思是所有的\(Q,K,V\)来自于同一个序列，对于SDPA中\(Q,K,V\)相同，对于MHA，\(Q,K,V\)相同但是会经过不同的线性层变换。

Fig. 4. self-attention. 图片来自博客

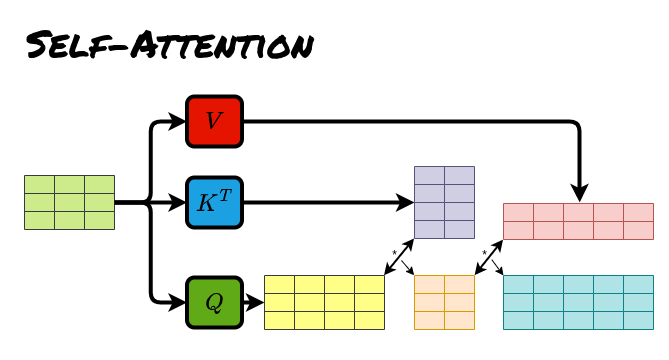
cross-attention

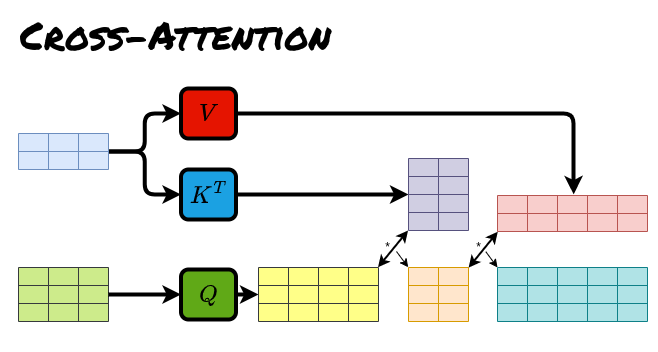
cross-attention意思是\(Q\)和\(K,V\)来自于不同的序列，换句话说，交叉注意力机制将两个具有相同维度的不同嵌入序列组合在一起，从一个序列中获取查询，从另一个序列中获取键和值。

Fig. 5. cross-attention. 图片来自博客

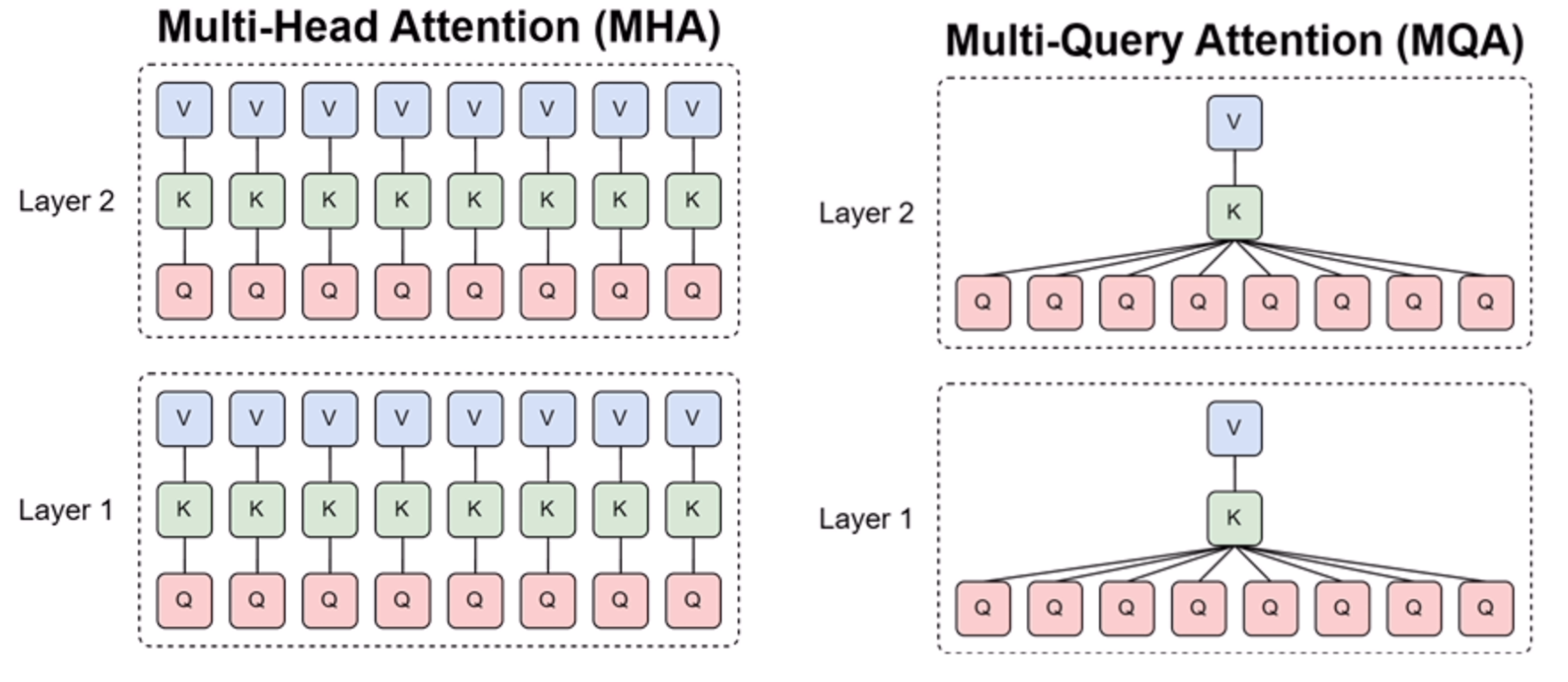
Mulit-Query Attention(MQA)

MQA的思路很简单，直接让所有Attention Head共享同一个\(K,V\)，是为了解决MHA中KV Cache过大的问题，MQA直接将KV cache减少到了MHA的\(\frac{1}{h}\),体现在公式上是:

\[\begin{aligned} \operatorname{MultiHead}(Q, K, V) & =\operatorname{Concat}\left(\operatorname{head}_1, \ldots, \operatorname{head}_{\mathrm{h}}\right) W^O \end{aligned}\]

\begin{equation} \label{eq:6} \begin{aligned} \text { where head } =\operatorname{Attention}\left(Q Wi^Q, K W{shared}^K, V W_{shared}^V\right) \end{aligned} \end{equation}

Fig. 6. MAQ. 图片来自博客

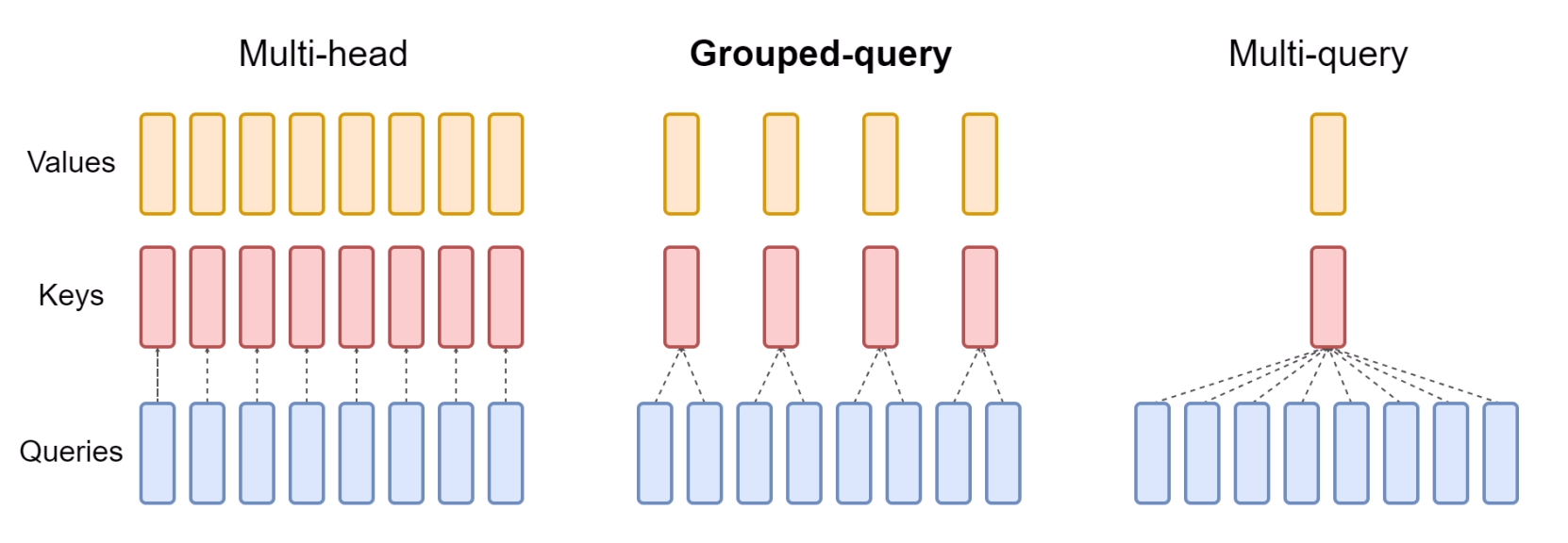
Group Query Attention(GQA)

然而，也有人担心MQA对KV Cache的压缩太严重，以至于会影响模型的学习效率以及最终效果。为此，一个MHA与MQA之间的过渡版本GQA（Grouped-Query Attention）应运而生。事后看来，GQA的思想也很朴素，它就是将所有Head分为g个组（g可以整除h），每组共享同一对K、V，g=h的时候就是MHA，g=1的时候是MQA.

Fig. 7. GQA.

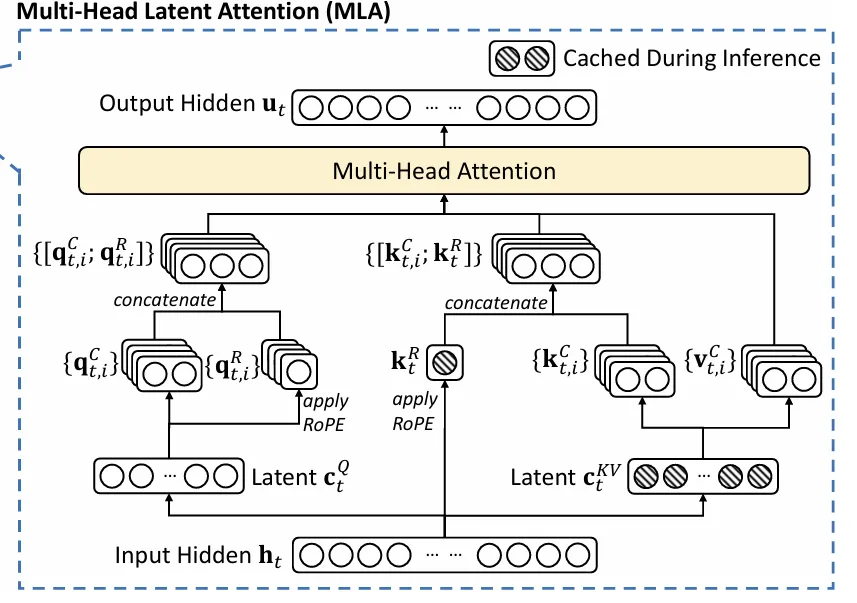
Multi-Latent Attention(MLA)

MLA可以参考苏神的文章了解详细的推导和解释 的性能优于 MHA，同时显著降低了 KV 缓存增强推理效率。MLA 不会像 MQA 和 GQA 那样减少 KV 头，而是将键和值联合压缩为潜空间量。

Fig. 8. MLA.

怎么做？

大概了解清楚了Attention，我们以MultiHeadAttention为例来分析一下Attention的计算。首先介绍一下符号这里以MHA为例，不考虑其他类型Attention，\(Q\)和\(K\)的head数一样，sequence length可能不一样， 其中\(D = NH\) ：

\[\begin{array}{l|l} \text { symbol } & \text { dimension } \\ \hline \text { B } & \text { batch } \\ { S_q } & \text { sequence length (query) } \\ { S_k } & \text { sequence length (key value) } \\ \text { D } & \text { d_model, embedding dimension } \\ \text { H } & \text { attention head dimension } \\ \text{N} & \text { number of heads } \\ \end{array}\]

实际运算过程如下：

Fig. 9. MHA的运算.

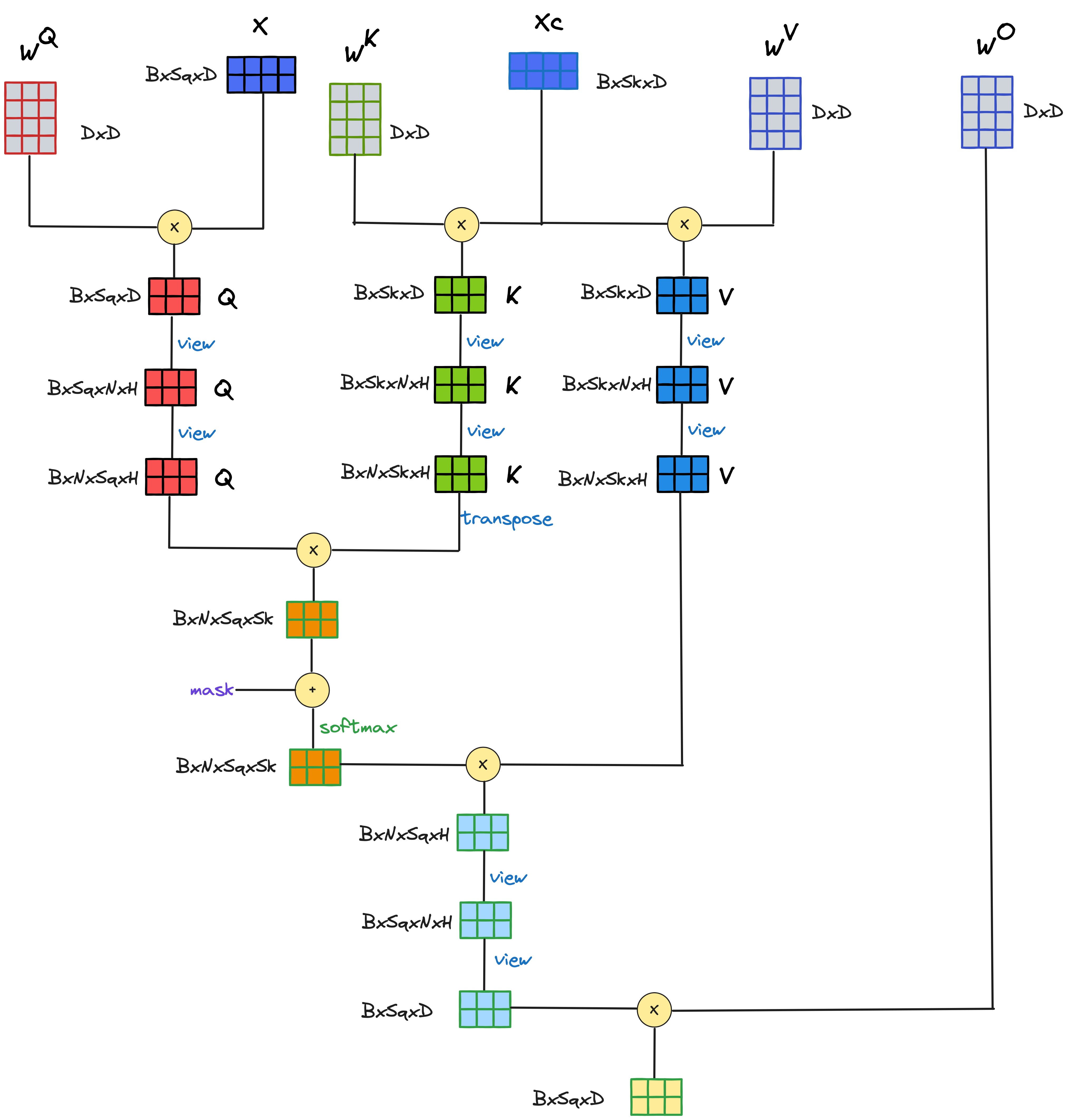
需要注意的是实际运算过程中\(B\)和\(N\)维度都是循环的维度，实际是\(S \times H\)和\(H\times S\)的矩阵运算，因此在\(Q \times K^T\)的矩阵之后的结果是attention score， 这个矩阵的维度是\(B \times N \times S \times S\)，本人一开始把输入矩阵当成\(B \times S \times D\)来看，实际算出来的attention score的矩阵维度是\(B \times S \times D\)和\(B \times D \times S\)的矩阵乘法，结果维度是\(B \times S \times S\)，这个是\({\color{red}不对的}\)。

关于计算量

首先定义向量 \(x\),\(y\) 和 矩阵 \(A\),\(B\) 具有如下shapesee the awesome How To Scale Your Model :

\[\def \red#1{\textcolor{red}{#1}} \def \green#1{\textcolor{green}{#1}} \def \blue#1{\textcolor{blue}{#1}} \def \purple#1{\textcolor{purple}{#1}} \def \orange#1{\textcolor{orange}{#1}} \def \gray#1{\textcolor{gray}{#1}} \begin{array}{cc} \textrm{array} & \textrm{shape} \\ \hline x & \textrm{[P]} \\ y & \textrm{[P]} \\ A & \mathrm{[N \times P]} \\ B & \mathrm{[P \times M]} \\ \hline \end {array}\]
  • 向量点积 \(x \cdot y\) 需要 \(P\) 个乘加运算, 或者说总共 \(2P\) 个浮点运算.
  • 矩阵和向量乘法 \(Ax\) 需要 \(N\) 个沿着\(A\)的行方向的点积, 也就是 \(2NP\) 个浮点运算.
  • 矩阵和矩阵的乘法 \(AB\) 需要 \(M\) 个沿着矩阵\(B\)列方向的矩阵和向量乘法, 也就是 \(2NPM\) 个浮点运算.
  • 总的来说，如果两个高维数组 \(C\) and \(D\), 它们的维度有些 CONTRACTING ，有些 BATCHING. (e.g. \(C[\blue{GH}IJ\red{KL}], D[\blue{GH}MN\red{KL}]\)) 那么它们的计算量就是2倍所有维度的乘积, (e.g. \(2\blue{GH}IJMN\red{KL}\)). 其中batch维度只乘一次. (Note also that the factor of 2 won’t apply if there are no contracting dimensions and this is just an elementwise product.)
\[\begin{array}{ccc} \textrm{Operation} & \textrm{FLOPs} & \textrm{Data} \\ \hline x \cdot y & 2P & 2P \\ A x & 2NP & NP + P \\ AB & 2NPM & NP + PM \\ [c_0,...,c_N] \cdot [d_0,...,d_N] & 2 \prod c_i \times \prod_{\substack{d_j \notin \blue{BATCH} \\ d_j \notin \red{CONTRACT}}} d_j & \prod c_i + \prod d_j \\ \hline \end {array}\]

需要注意的是，对于矩阵乘法，计算量是立方级\(O(N^3)\)的而数据传输量仅是平方级的\(O(N^2)\) ——这意味着随着矩阵乘法规模的扩大，更容易达到计算饱和极限。这非常不寻常，也在很大程度上解释了为什么我们使用以矩阵乘法为主的架构——它们易于扩展。

Fig. 10. 矩阵乘法的flops.

因此对于MHA来说计算量如下，分为两个部分去计算：

其中\(QKVO\)的线性层的计算如下其中训练过程的flops计算包含backward中两个链式导数相乘加上forward的矩阵乘总共三个矩阵乘所以是\(6NPM\)的flops，参考 How To Scale Your Model-(Forward and reverse FLOPs) ：

\[\begin{array}{ccc} \textrm{operation} & \textrm{train FLOPs} & \textrm{inference FLOPs} &\textrm{params} \\ \hline \\ A[B,S_q,\red{D}] \cdot W_{Q}[\red{D}, D] & 6B{S_q}DD & 2B{S_q}DD & DD \\[10pt] A[B,S_k,\red{D}] \cdot W_{K}[\red{D}, D] & 6B{S_k}DD & 2B{S_k}DD & DD \\[10pt] A[B,S_k,\red{D}] \cdot W_{V}[\red{D}, D] & 6B{S_k}DD & 2B{S_k}DD & DD \\[10pt] A[B,S_q,\red{D}] \cdot W_{O}[\red{D}, D] & 6B{S_q}DD & 2B{S_q}DD & DD \\[10pt] \hline \\ & 12BD({S_q}+{S_k})D& 4BD({S_q}+{S_k})D & 4DD \end{array}\]

对于\(Q\)和\(K\)矩阵乘，就像之前说的\(Q\)和\(K\)的矩阵运算在\(B\)和\(N\)维度循环，在\(S_k\)或者\(S_q\)及\(H\)维度相乘。

\[\begin{array}{cc} \textrm{operation} & \textrm{train FLOPs} & \textrm{inference FLOPs}\\ \hline \\[3pt] Q[\blue{B}, \blue{N}, {S_q}, \red{H}] \cdot K[\blue{B}, \blue{N}, S_k, \red{H}] & 6BN{S_q}{S_k}H & 2BN{S_q}{S_k}H \\[3pt] \textrm{softmax}_S \;\; L[B, N, S_q, S_k] & \gray{O(BN{S_q}{S_k})} & \gray{O(BN{S_q}{S_k})} \\[3pt] S[\blue{B}, \blue{N}, \red{S_q}, \red{S_k}] \cdot V[\blue{B}, \blue{N}, \red{S_k}, \red{H}] & 6BN{S_q}{S_k}H & 2BN{S_q}{S_k}H\\[3pt] \hline \\ & \approx 12BN{S_q}{S_k}H = 12B{S_q}{S_k}D & \approx 4BN{S_q}{S_k}H = 4B{S_q}{S_k}D \\ \end{array}\]

总体来说，MHA的计算量如下：

\[\begin{array}{ccc} \textrm{ } & \textrm{train FLOPs} & \textrm{inference FLOPs} &\textrm{params} \\ \hline \\ MHA & 12BD({S_q}+{S_k})D + 12B{S_q}{S_k}D & 4BD({S_q}+{S_k})D + 4B{S_q}{S_k}D & 4DD \\[10pt] \hline \\ & \end{array}\]